Trong không gian \(Oxyz,\) cho mặt cầu \(\left( S \right):\;{\left( {x - 2} \right)^2} + {\left( {y - 3} \right)^2} + {\left( {z + 1} \right)^2} = 16\) và điểm \(A\left( { - 1; - 1; - 1} \right).\) Xét các điểm \(M\) thuộc \(\left( S \right)\) sao cho đường thẳng \(AM\) tiếp xúc với \(\left( S \right),\;M\) luôn thuộc mặt phẳng có phương trình là:
Phương pháp giải
Tập hợp các điểm của tiếp tuyến từ 1 điểm A nằm ngoài mặt cầu là một đường tròn
Lời giải của Tự Học 365
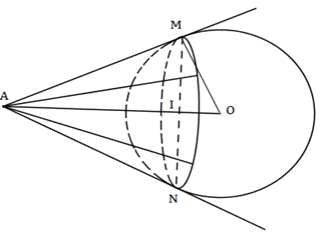
Ta có\(\left( S \right)\) có tâm \(O\left( {2;\;3; - 1} \right)\) và bán kính \(R = 4.\)
\(\overrightarrow {AO} = \left( {3;\;4;\;0} \right) \Rightarrow OA = 5.\)
Tập hợp các điểm \(M\) là đường tròn tâm \(I\) bán kính \(IM.\)
Gọi \(\left( \alpha \right)\) là mặt phẳng chứa đường tròn đó.
Khi đó ta có \(OA \bot \left( \alpha \right) \Rightarrow \left( \alpha \right)\) nhận \(\overrightarrow {AO} = \left( {3;\;4;\;0} \right)\) làm VTPT.
\( \Rightarrow \left( \alpha \right):\;\;3x + 4y + a = 0.\)
Áp dụng hệ thức lượng trong tam giác vuông \(OAM\) có đường cao \(MI\) ta có:
\(\begin{array}{l}OI = \dfrac{{O{M^2}}}{{OA}} = \dfrac{{{4^2}}}{5} = \dfrac{{16}}{5} = d\left( {O;\;\left( \alpha \right)} \right).\\ \Rightarrow \dfrac{{16}}{5} = \dfrac{{\left| {2.3 + 4.3 + a} \right|}}{5} \Leftrightarrow \left| {18 + a} \right| = 16 \Leftrightarrow \left[ \begin{array}{l}a = - 2\\a = - 34\end{array} \right..\\ \Rightarrow \left[ \begin{array}{l}\left( \alpha \right):\;\;3x + 4y - 2 = 0\\\left( \alpha \right):\;3x + 4y - 34 = 0\end{array} \right..\end{array}\)
Đáp án cần chọn là: a
Toán Lớp 12
