Lời giải của Tự Học 365

Miền nghiệm của hệ \(\left\{ {\begin{array}{*{20}{c}}{y - 2x \le 2}\\{2y - x \ge 4}\\{x + y \le 5}\end{array}} \right.\) là miền trong của tam giác $ABC$ kể cả biên (như hình)

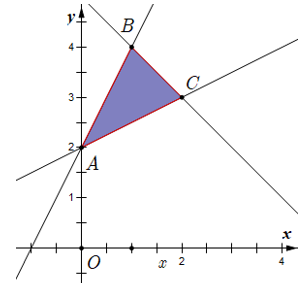
Ta thấy \(F = y - x\) đạt giá trị nhỏ nhất chỉ có thể tại các điểm \(A\), \(B\), \(C\).

Tại \(A\left( {0; 2} \right)\) thì \(F = 2\).

Tại \(B\left( {1; 4} \right)\) thì \(F = 3\)

Tại \(A\left( {2; 3} \right)\) thì \(F = 1\).

Vậy \(\min F = 1\) khi \(x = 2\), \(y = 3\).

Đáp án cần chọn là: a