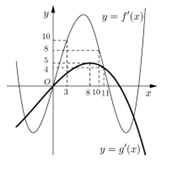
Cho hai hàm số \(y = f\left( x \right),\;y = g\left( x \right).\) Hai hàm số \(y = f'\left( x \right)\) và \(y = g'\left( x \right)\) có đồ thị hàm như hình vẽ bên, trong đó đường cong đậm hơn là đồ thị của hàm số \(y = g'\left( x \right).\) Hàm số \(h\left( x \right) = f\left( {x + 6} \right) - g\left( {2x + \dfrac{5}{2}} \right)\) đồng biến trên khoảng nào dưới đây?
Phương pháp giải
- Tính đạo hàm \(h'\left( x \right)\)
- Hàm số \(y = h\left( x \right)\) đồng biến \( \Leftrightarrow h'\left( x \right) \ge 0.\)
- Tìm một khoảng mà $h(x)$ đồng biến rồi kiểm tra xem các khoảng ở mỗi đáp án có nằm trong khoảng vừa tìm được hay không rồi kết luận.
Lời giải của Tự Học 365
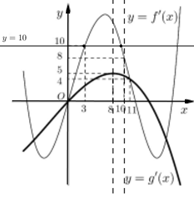
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 10\) cắt đồ thị hàm số \(y = f'\left( x \right)\) tại hai điểm phân biệt \(\left( {3;\;10} \right)\) và \(\left( {m;\;10} \right)\) với mọi \(m \in \left( {8;\;10} \right).\)
Xét \(\left\{ \begin{array}{l}f'\left( {x + 6} \right) > 10\\g'\left( {2x + \dfrac{5}{2}} \right) \le 5\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}3 < x + 6 < m < 8\\0 \le 2x + \dfrac{5}{2} \le 11\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 3 < x < 2\\ - \dfrac{5}{4} \le x \le \dfrac{{17}}{4}\end{array} \right. \) \(\Leftrightarrow - \dfrac{5}{4} \le x < 2.\)
Lại có \(h\left( x \right)\) đồng biến \( \Leftrightarrow h'\left( x \right) > 0 \Leftrightarrow f'\left( {x + 6} \right) - 2g'\left( {2x + \dfrac{5}{2}} \right) > 0\)
Mà \(f'\left( {x + 6} \right) > 10\) và \(-2g'\left( {2x + \dfrac{5}{2}} \right) \ge -10 \) trên \(\left[ { - \dfrac{5}{4};\;2} \right)\) \(\Rightarrow h\left( x \right)\) đồng biến trên \(\left[ { - \dfrac{5}{4};\;2} \right).\)
Dựa vào các đáp án ta thấy đáp án B thỏa mãn.
Đáp án cần chọn là: b
Toán Lớp 12
