Cho hình chóp \(S.ABCD\) có đáy là hình chữ nhật, biết \(AB = 2a,\,\,AD = a,\,\,SA = 3a\) và \(SA\) vuông góc với mặt phẳng đáy. Gọi \(M\) là trung điểm cạnh \(CD\). Khoảng cách giữa hai đường thẳng \(SC\) và \(BM\) bằng:
Phương pháp giải
Đặt hệ trục tọa độ. Sử dụng công thức tính khoảng cách giữa hai đường thẳng chéo nhau \(d\left( {SC;BM} \right) = \dfrac{{\left| {\left[ {\overrightarrow {SC} ;\overrightarrow {BM} } \right].\overrightarrow {SB} } \right|}}{{\left| {\left[ {\overrightarrow {SC} ;\overrightarrow {BM} } \right]} \right|}}\).
Lời giải của Tự Học 365
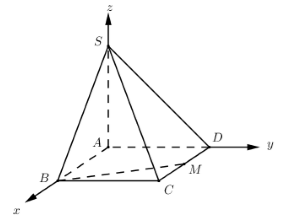
Đặt hệ trục toa độ như hình vẽ, chọn \(a = 1\). Khi đó ta có:
\(A\left( {0;0;0} \right),\,\,B\left( {2;0;0} \right),\,\,C\left( {2;1;0} \right);\,\,D\left( {0;1;0} \right);\,\,S\left( {0;0;3} \right)\).
\(M\) là trung điểm cạnh \(CD \Rightarrow M\left( {1;1;0} \right)\).
Ta có \(\overrightarrow {SC} = \left( { - 2; - 1;3} \right);\,\,\overrightarrow {BM} = \left( { - 1;1;0} \right);\,\,\overrightarrow {SB} = \left( {2;0; - 3} \right)\) \( \Rightarrow \left[ {\overrightarrow {SC} ;\overrightarrow {BM} } \right] = \left( { - 3; - 3; - 3} \right)\).
\( \Rightarrow d\left( {SC;BM} \right) = \dfrac{{\left| {\left[ {\overrightarrow {SC} ;\overrightarrow {BM} } \right].\overrightarrow {SB} } \right|}}{{\left| {\left[ {\overrightarrow {SC} ;\overrightarrow {BM} } \right]} \right|}} = \dfrac{{\left| { - 3.2 - 3.0 + \left( { - 3} \right).\left( { - 3} \right)} \right|}}{{\sqrt {{{\left( { - 3} \right)}^2} + {{\left( { - 3} \right)}^2} + {{\left( { - 3} \right)}^2}} }} = \dfrac{3}{{3\sqrt 3 }} = \dfrac{{\sqrt 3 }}{3}\).
Đáp án cần chọn là: c
Toán Lớp 12
