Lời giải của Tự Học 365

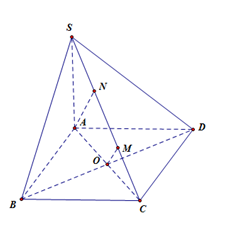
Ta có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right)$.

Khi đó $\widehat {\left( {\left( {SBC} \right);\left( {ABCD} \right)} \right)} = \widehat {SBA} = {60^0}$

Suy ra $SA = AB\tan {60^0} = a\sqrt 3 $.

Gọi $O$ là tâm hình vuông $ABCD$ ta có:

$\left\{ \begin{array}{l}BD \bot AC\\BD \bot SA\end{array} \right. \Rightarrow BD \bot \left( {SAC} \right)$

Trong $(SAC)$ dựng $OM \bot SC\,\,\left( 1 \right)$ ta có : \(OM \subset \left( {SAC} \right) \Rightarrow OM \bot BD\,\,\left( 2 \right)\) . Từ (1) và (2) suy ra $OM$ là đường vuông góc chung $BD$ và $SC$.

Ta có $\Delta CAS \backsim \Delta CMO\;\;\left( {g - g} \right)$

$\Rightarrow \dfrac{{SC}}{{CO}} = \dfrac{{SA}}{{MO}} \Rightarrow OM = \dfrac{{SA.OC}}{{SC}}$

$ = \dfrac{{a\sqrt 3 .\dfrac{{a\sqrt 2 }}{2}}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{a\sqrt 6 }}{{2\sqrt 5 }} = \dfrac{{a\sqrt {30} }}{{10}}.$

Đáp án cần chọn là: d