Lời giải của Tự Học 365

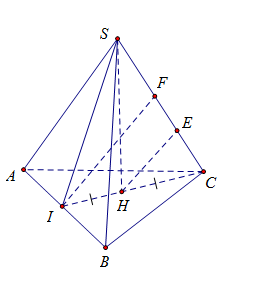
Ta có $\left\{ \begin{array}{l}CI \bot AB\\SH \bot AB\end{array} \right. \Rightarrow AB \bot \left( {SIC} \right)$

Dựng $IF \bot SC\,\,\left( 1 \right)$ khi đó \(IF \subset \left( {SIC} \right) \Rightarrow IF \bot AB\,\,\left( 2 \right)\), do đó  $IF$ là đoạn vuông góc chung của $AB$ và $SC$. Dựng $HE \bot SC \Rightarrow HE//IF$ ta có: $HE = \dfrac{1}{2}IF$

Lại có $CI = \dfrac{{a\sqrt 3 }}{2} \Rightarrow CH = \dfrac{{a\sqrt 3 }}{4}$

Khi đó

$HE = \dfrac{{SH.HC}}{{\sqrt {S{H^2} + C{H^2}} }} = \dfrac{{a\sqrt 3 .\dfrac{{a\sqrt 3 }}{4}}}{{\sqrt {{{\left( {a\sqrt 3 } \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{4}} \right)}^2}} }} = \dfrac{{a\sqrt {51} }}{{17}} \Rightarrow IF = \dfrac{{2a\sqrt {51} }}{{17}}$.

Đáp án cần chọn là: c