Cho hàm số \(y=f\left( x \right)\) có bảng biến thiên như sau:
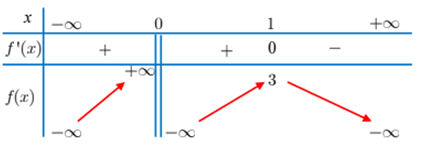
Với các giá trị thực của tham số \(m\), phương trình \(f\left( x \right)=m\) có nhiều nhất bao nhiêu nghiệm?
Phương pháp giải
Số nghiệm của phương trình bằng số giao điểm của đường thẳng \(y = m\) với đồ thị hàm số \(y = f\left( x \right)\).
Lời giải của Tự Học 365
Quan sát đồ thị hàm số ta thấy:
+) Với \(m < 3\) thì đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại \(3\) điểm phân biệt.
+) Với \(m = 3\) thì đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại \(2\) điểm phân biệt.
+) Với \(m > 3\) thì đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại duy nhất \(1\) điểm.
Vậy đường thẳng \(y = m\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại nhiều nhất \(3\) điểm.
Do đó phương trình đã cho có nhiều nhất \(3\) nghiệm.
Đáp án cần chọn là: d
Toán Lớp 12
