Cho hàm số $y = f\left( x \right)$ xác định trên $R\backslash \left\{ { - 1;\,1} \right\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên sau:
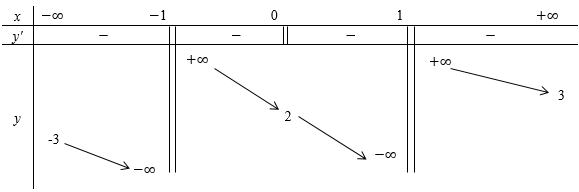
Tìm tất cả các giá trị thực của tham số m sao cho đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt.
Phương pháp giải
- Biện luận số nghiệm của phương trình dựa vào số giao điểm của đường thẳng và đường cong vừa vẽ được.
Lời giải của Tự Học 365
Quan sát BBT ta thấy đường thẳng $y = 2m + 1$ cắt đồ thị hàm số $y = f\left( x \right)$ tại hai điểm phân biệt $ \Leftrightarrow \left[ \begin{gathered}2m + 1 < - 3 \hfill \\ 2m + 1 > 3 \hfill \\ \end{gathered} \right. \Leftrightarrow \left[ \begin{gathered} m < - 2 \hfill \\ m > 1 \hfill \\ \end{gathered} \right.$ .
Đáp án cần chọn là: c
Toán Lớp 12
