Cho hàm số \(y=\dfrac{ax+b}{cx+1}\) có bảng biến thiên:
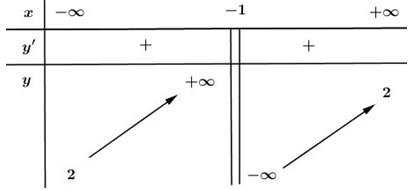
Xét các mệnh đề:
\(\begin{align} & \left( 1 \right)\,\,\,\,\,c=1 \\ & \left( 2 \right)\,\,\,\,a=2 \\ \end{align}\)
(3) Hàm số đồng biến trên \(\left( -\infty ;-1 \right)\cup \left( -1;+\infty \right).\)
(4) Nếu \(y'=\frac{1}{{{\left( x+1 \right)}^{2}}}\) thì \(b=1.\)
Tìm số mệnh đề đúng trong các mệnh đề trên.
Phương pháp giải
Dựa vào BBT để kết luận tính đơn điệu của hàm số và suy ra các giá trị a, c tương ứng.
Lời giải của Tự Học 365
TXĐ: \(D=R\backslash \left\{ -\frac{1}{c} \right\}.\)
Ta có: \(y'=\frac{a-bc}{{{\left( cx+1 \right)}^{2}}}.\)
Ta thấy đồ thị có TCĐ \(x=-1\Rightarrow -\frac{1}{c}=-1\Rightarrow c=1\Rightarrow \) Mệnh đề (1) đúng.
Hàm số có TCN \(y=2\Rightarrow \frac{a}{c}=2\Leftrightarrow a=2c=2\Rightarrow \) Mệnh đề (2) đúng.
Theo BBT ta thấy hàm số đồng biến trên từng khoảng xác định của hàm số.
\(\Rightarrow y'>0\Leftrightarrow a-bc>0\) do \({{\left( cx+1 \right)}^{2}}>0\,\,\,\forall x\in D \)
\(\Rightarrow \) Hàm số đồng biến trên \(\left( -\infty ;\,\,-1 \right)\) và \(\left( -1;+\infty \right)\Rightarrow \) Mệnh đề (3) sử dụng kí hiệu hợp nên sai.
Nếu \(y'=\frac{1}{{{\left( x+1 \right)}^{2}}}\Rightarrow \frac{a-bc}{{{\left( cx+1 \right)}^{2}}}=\frac{1}{{{\left( x+1 \right)}^{2}}}\)
\(\begin{align} & \Leftrightarrow \frac{2-b}{{{\left( x+1 \right)}^{2}}}=\frac{1}{{{\left( x+1 \right)}^{2}}}\Leftrightarrow 2-b=1 \\ & \Leftrightarrow b=1. \\ \end{align}\)
\(\Rightarrow \) Mệnh đề (4) đúng.
Như vậy có 3 mệnh đề đúng.
Đáp án cần chọn là: a
Toán Lớp 12
