Lời giải của Tự Học 365

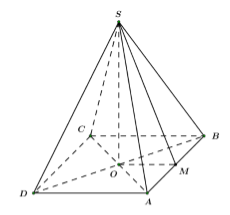
Gọi \(O\) là giao điểm của \(AC\) và \(BD.\)

\(SABCD\) là hình chóp đều \( \Rightarrow SO \bot \left( {ABCD} \right).\)

Ta có: \(\left( {SAB} \right) \cap \left( {ABCD} \right) = \left\{ {AB} \right\}.\)

Gọi \(M\) là trung điểm của \(AB.\)

Ta có:\(OM \bot AB\,\,\left( {OM//AD,\,\,AD \bot AB} \right)\)

\(SM \bot AB\)  do \(\Delta SAB\) là tam giác cân tại \(S.\)

\( \Rightarrow \angle \left( {\left( {SAB} \right),\,\,\left( {ABCD} \right)} \right) = \angle \left( {SM,\,\,OM} \right) = \angle SMO.\)

Ta có: \(SM = \sqrt {S{A^2} - M{A^2}}  = \sqrt {5{a^2} - {a^2}}  = 2a.\) (Định lý Pitago)

\(OM = \dfrac{1}{2}AD = a.\)

\(\begin{array}{l} \Rightarrow \cos SMO = \dfrac{{OM}}{{SM}} = \dfrac{a}{{2a}} = \dfrac{1}{2}\\ \Rightarrow \angle SMO = {60^0}.\end{array}\)

Đáp án cần chọn là: c