Cho tứ diện \(ABCD\) có \(AB = CD = 4,BC = AD = 5,AC = BD = 6\). \(M\) là điểm thay đổi trong tâm giác \(ABC\). Các đường thẳng qua \(M\) song song với \(AD,BD,CD\) tương ứng cắt mặt phẳng \(\left( {BCD} \right),\left( {ACD} \right),\left( {ABD} \right)\) tại \(A',B',C'\). Giá trị lớn nhất của \(MA'.MB'.MC'\) là
Phương pháp giải
- Kéo dài \(AM,BM,CM\) cắt các đoạn thẳng \(BC,CA,AB\) lần lượt tại \(H,G,F\).
- Dựng các đường thẳng qua \(M\) và song song với \(AD,BD,CD\) suy ra các điểm \(A',B',C'\).
- Sử dụng định lý Ta – let tính \(MA',MB',MC'\).

- Sử dụng hệ thức \(\dfrac{{{A_1}M}}{{AM}} + \dfrac{{{B_1}M}}{{BM}} + \dfrac{{{C_1}M}}{{CM}} = 1\) đánh giá GTLN của tích \(MA'.MB'.MC'\).
ở đó, \(M\) là một điểm nằm trong tam giác \(ABC\) và \({A_1},{B_1},{C_1}\) lần lượt là các giao điểm của \(AM,BM,CM\) với các cạnh \(BC,CA,AB\).
Lời giải của Tự Học 365
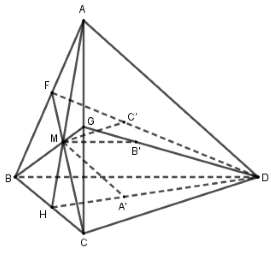
Trong tam giác \(ABC\), kéo dài \(AM,BM,CM\) cắt các đoạn thẳng \(BC,CA,AB\) lần lượt tại \(H,G,F\).
+) Trong mặt phẳng \(\left( {HAD} \right)\), kẻ \(MA'//AD\).
+) Trong mặt phẳng \(\left( {GBD} \right)\), kẻ \(MB'//BD\).
+) Trong mặt phẳng \(\left( {FCD} \right)\), kẻ \(MC'//CD\).
Từ đó ta được các điểm \(A',B',C'\) cần tìm.
Theo định lý Ta – let ta có: \(\dfrac{{MA'}}{{AD}} = \dfrac{{HM}}{{HA}} \Rightarrow MA' = 5.\dfrac{{MH}}{{AH}}\)
\(\dfrac{{MB'}}{{BD}} = \dfrac{{GM}}{{GB}} \Rightarrow MB' = 6.\dfrac{{MG}}{{BG}}\); \(\dfrac{{MC'}}{{CD}} = \dfrac{{FM}}{{FC}} \Rightarrow MC' = 4.\dfrac{{MF}}{{CF}}\)
\( \Rightarrow MA'.MB'.MC' = 120.\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}}\).
Trong tam giác \(ABC\) ta có: \(1 = \dfrac{{MH}}{{AH}} + \dfrac{{MG}}{{BG}} + \dfrac{{MF}}{{CF}} \ge 3\sqrt[3]{{\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}}}}\) \( \Rightarrow \dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}} \le \dfrac{1}{{27}}\)
Do đó \(MA'.MB'.MC' = 120.\dfrac{{MH}}{{AH}}.\dfrac{{MG}}{{BG}}.\dfrac{{MF}}{{CF}} \le 120.\dfrac{1}{{27}} = \dfrac{{40}}{9}\)\( \Rightarrow {\left( {MA'.MB'.MC'} \right)_{\max }} = \dfrac{{40}}{9}\)
Đáp án cần chọn là: a
Toán Lớp 12
