Lời giải của Tự Học 365

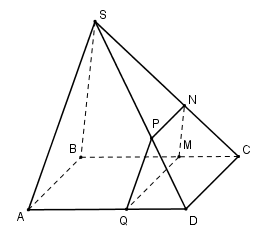
Vì $MN // BS $ nên \(\dfrac{{CN}}{{CS}} = \dfrac{{CM}}{{CB}}\) (Định lí Ta – let)  (1)

Vì $MQ // CD // AB$ nên \(\dfrac{{CM}}{{CB}} = \dfrac{{DQ}}{{DA}}\)                   (2)

Vì $NP // CD$ nên \(\dfrac{{CN}}{{CS}} = \dfrac{{DP}}{{DS}}\) (Định lí Ta – let)    (3)

Từ (1), (2) và (3) suy ra \(\dfrac{{DP}}{{DS}} = \dfrac{{DQ}}{{DA}}\) \( \Rightarrow PQ // SA\)  (Định lí Ta – let đảo)

Ta có: \(SA \subset \left( {SAB} \right)\,\,;\,\,SA \subset \left( {SAD} \right)\).

Tuy nhiên $PQ \subset \left( {SAD} \right)$ nên $PQ$ không song song với $mp(SAD).$

Ngoài ra $PQ$ không nằm trong $(SAB)$ nên $PQ//(SAB)$

Vậy $PQ // (SAB).$

Đáp án cần chọn là: b