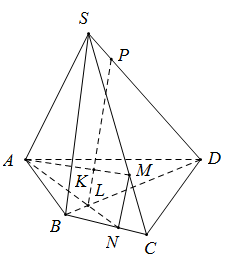
Cho hình chóp $S.ABCD $ có $M, N$ lần lượt nằm trên các cạnh $SC, BC.$ Gọi $P$ là giao điểm của $SD$ với mặt phẳng $(AMN).$ $L$ là giao $AN$ và $BD.$ $K$ là giao $AM$ và $LP.$ Khẳng định nào sau đây đúng?
Phương pháp giải
- Xét tính đúng sai của từng đáp án dựa vào các quan hệ điểm thuộc đường thẳng, điểm thuộc mặt phẳng.
- Sử dụng phương pháp tìm giao tuyến của hai mặt phẳng để tìm giao tuyến hai mặt phẳng \(\left( {AMN} \right)\) và \(\left( {SBD} \right)\).
Lời giải của Tự Học 365
Vì $L$ là giao của $AN$ và $BD$ nên $L ∈ BD$
$⇒ L ∈ (SBD)$
Có $P ∈ SD ⇒ P ∈ (SBD)$
$ \Rightarrow LP \subset \left( {SBD} \right) \Rightarrow KL \subset \left( {SBD} \right)$
Vì $K ∈ AM; L ∈ AN ⇒ KL ⊂ (AMN)$
Vậy $KL$ là giao tuyến của $(AMN) $ và $(SBD)$
Đáp án cần chọn là: c
Toán Lớp 12
