Lời giải của Tự Học 365

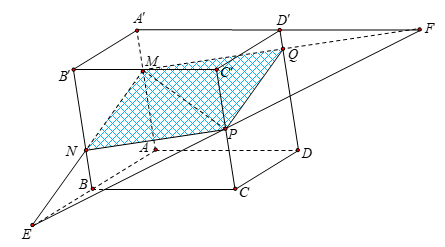
Ta có \(\left\{ \begin{array}{l}\left( {BB'C'C} \right)\,{\rm{//}}\,\left( {AA'D'D} \right)\\\left( {MNP} \right) \cap \left( {BB'C'C} \right) = NP\\\left( {MNP} \right) \cap \left( {AA'D'D} \right) = MQ\end{array} \right. \Rightarrow NP\,{\rm{//}}\,MQ\).

Tương tự: \(\left\{ \begin{array}{l}\left( {AA'B'B} \right)\,{\rm{//}}\,\left( {CC'D'D} \right)\\\left( {MNP} \right) \cap \left( {AA'B'B} \right) = MN\\\left( {MNP} \right) \cap \left( {CC'D'D} \right) = PQ\end{array} \right. \Rightarrow MN\,{\rm{//}}\,PQ\)

Suy ra mặt phẳng \(\left( {MNP} \right)\) cắt hình hộp theo thiết diện là hình bình hành \(MNPQ\).

Mặt khác \(\left\{ \begin{array}{l}BN = \dfrac{1}{3}BB' = \dfrac{1}{3}AA'\\AM = \dfrac{2}{3}AA'\end{array} \right. \Rightarrow \dfrac{{BN}}{{AM}} = \dfrac{1}{2}\).

Trong mặt phẳng \(\left( {ABB'A'} \right)\), gọi \(E\) là giao điểm của hai đường thẳng \(MN\) và \(AB\) thì \(BN\) là đường trung bình của tam giác \(AME\) \( \Rightarrow N\) là trung điểm của đoạn thẳng \(ME\).

Trong mặt phẳng \(\left( {MNPQ} \right)\), gọi \(F\) là giao điểm của \(EP\) và \(MQ\) thì \(NP\) là đường trung bình của tam giác $MEF$ (vì \(NP\,{\rm{//}}\,MQ\) và \(N\) là trung điểm \(EM\)) \( \Rightarrow NP = \dfrac{1}{2}MF\)

Mà tứ giác \(MNPQ\) là hình bình hành nên \(NP = MQ \Rightarrow Q\) là trung điểm \(MF\) hay \(\dfrac{{FQ}}{{FM}} = \dfrac{1}{2}\)

Lại có \(D'Q\,{\rm{//}}\,A'M \Rightarrow \dfrac{{D'Q}}{{A'M}} = \dfrac{{FQ}}{{FM}} = \dfrac{1}{2}\)

\( \Leftrightarrow \dfrac{{D'Q}}{{\dfrac{1}{3}AA'}} = \dfrac{1}{2} \Leftrightarrow \dfrac{{D'Q}}{{DD'}} = \dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6}\)

Đáp án cần chọn là: a