Cho tứ diện \(ABCD\). Gọi \(M\), \(N\) lần lượt là trọng tâm của các tam giác \(ABC\), \(ABD\)
Những khẳng định nào sau là đúng?
\(\left( 1\right)\,:MN\;{\rm{//}}\;\left( {BCD} \right)\);
\(\left( 2\right)\,:MN\;{\rm{//}}\;\left( {ACD} \right)\);
\(\left( 3\right)\,:MN\;{\rm{//}}\;\left( {ABD} \right)\).
Phương pháp giải
Sử dụng phương pháp chứng minh đường thẳng song song mặt phẳng (tìm một đường thẳng thuộc mặt phẳng mà song song với đường thẳng đã cho) để xét tính đúng sai cho từng khẳng định.
Lời giải của Tự Học 365
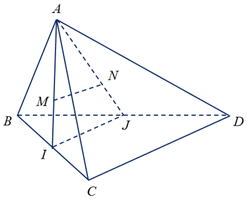
Gọi \(I\), \(J\) lần lượt là trung điểm \(BC\), \(BD\).
Ta có \(\dfrac{{AM}}{{AI}} = \dfrac{{AN}}{{{\rm{AJ}}}} = \dfrac{2}{3}\)\( \Rightarrow MN\;{\rm{//}}\;{\rm{IJ}}\) \( \Rightarrow MN\;{\rm{//}}\;IJ\;{\rm{//}}\;CD\) \( \Rightarrow \)\(MN\;{\rm{//}}\;\left( {BCD} \right)\) và \(MN\;{\rm{//}}\;\left( {ACD} \right)\).
Đáp án cần chọn là: c
Toán Lớp 12
