Cho hình chóp \(S.ABCD\) có đáy là hình bình hành. Giao tuyến của \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\) là
Phương pháp giải
Sử dụng định lý giao tuyến của ba mặt phẳng nếu không đồng quy thì song song, từ đó xác định đúng giao tuyến của hai mặt phẳng \(\left( {SAB} \right)\) và \(\left( {SCD} \right)\)
Lời giải của Tự Học 365
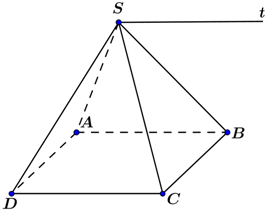
Xét ba mặt phẳng \(\left( {SAB} \right),\left( {SCD} \right),\left( {ABCD} \right)\) ta có:
\(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\\left( {SCD} \right) \cap \left( {ABCD} \right) = CD\\\left( {SAB} \right) \cap \left( {SCD} \right) = d\end{array} \right.\)
Mà \(AB//CD\) nên \(AB//CD//d\)
Ngoài ra, \(S \in \left( {SAB} \right) \cap \left( {SCD} \right) = d\) nên giao tuyến \(d\) chính là đường thẳng đi qua \(S\) và song song với \(AB,CD\)
Đáp án cần chọn là: b
Toán Lớp 12
