Lời giải của Tự Học 365

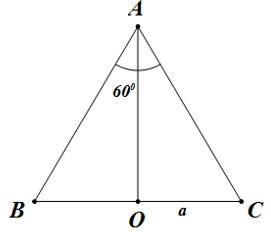
Giả sử thiết diện của mặt phẳng đi qua trục của hình nón với hình nón là tam giác \(ABC\), theo giả thiết bài toán, ta có \(ABC\) là tam giác đều cạnh \(2a\). Do đó hình nón có:

Bán kính đáy \(R = a\).

Độ dài đường sinh \(l = AC = 2a\).

Diện tích xung quanh cần tìm \({S_{xq}} = \pi Rl = \pi .a.2a = 2\pi {a^2}\).

Đáp án cần chọn là: d