Sóng truyền theo phương ngang trên một sợi dây dài với tần số \(15Hz\). Điểm M trên dây tại một thời điểm đang ở vị trí cao nhất và tại thời điểm đó điểm N cách M \(5cm\) đang đi qua vị trí có li độ bằng nửa biên độ và đi lên. Coi biên độ sóng không đổi khi truyền. Biết khoảng cách MN nhỏ hơn bước sóng của sóng trên dây. Chọn đáp án đúng cho tốc độ truyền sóng và chiều truyền sóng.
Phương pháp giải
+ Sử dụng vòng tròn lượng giác.
+ Vận dụng công thức tính độ lệch pha: \(\Delta \varphi = \dfrac{{2\pi \Delta d}}{\lambda }\)
+ Áp dụng công thức tính tốc độ truyền sóng: \(v = \lambda f\)
Lời giải của Tự Học 365
Ta có:
+ Điểm M ở vị trí cao nhất tức là biên dương.
+ Điểm N qua vị trí có li độ bằng \(\dfrac{A}{2}\) và đang đi lên
Vẽ trên vòng tròn lượng giác, ta được:
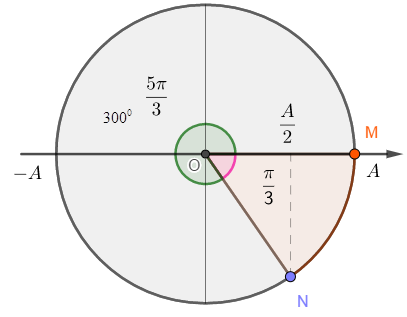
Ta có 2 trường hợp của góc lệch pha giữa M và N:
+ TH 1: M, N lệch pha nhau: \(\Delta \varphi = \dfrac{\pi }{3}\)
\(\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{\pi }{3}\\ \to \lambda = 6\Delta d = 6.5 = 30cm\\ \to v = \lambda f = 30.15 = 450cm/s = 4,5m/s\end{array}\)
M sớm pha hơn N => Sóng truyền từ M đến N
+ TH 2: M, N lệch pha nhau \(\Delta \varphi = \dfrac{{5\pi }}{3}\)
\(\begin{array}{l}\Delta {\varphi _{MN}} = \dfrac{{2\pi \Delta d}}{\lambda } = \dfrac{{5\pi }}{3}\\ \to \lambda = \dfrac{6}{5}\Delta d = \dfrac{6}{5}.5 = 6cm\\ \to v = \lambda f = 6.15 = 90cm/s\end{array}\)
Do N sớm pha hơn M
=> Sóng truyền từ N đến M
Đáp án cần chọn là: d
Vật lý Lớp 12
