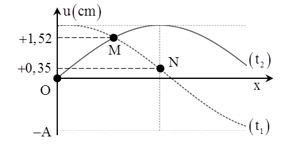
Trên một sợi dây dài có một sóng ngang, hình sin truyền qua. Hình dạng của một đoạn dây tại hai thời điểm \({t_1}\) và \({t_2}\) có dạng như hình vẽ bên. Trục Ou biểu diễn li độ của các phần tử M và N ở các thời điểm. Biết \({t_2} - {t_1} = 0,11s\) và nhỏ hơn một chu kì sóng. Chu kì dao động của sóng là:
Phương pháp giải
+ Đọc đồ thị và áp dụng các công thức sóng cơ học.
+ Sử dụng vòng tròn lượng giác
Lời giải của Tự Học 365
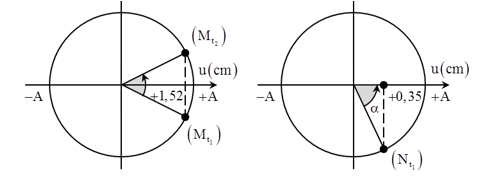
Từ đồ thị ta xác định được:
Tại \({t_1}\) : \(\left\{ \begin{array}{l}{u_M} = 1,52cm\\{u_N} = 0,35cm\end{array} \right.\)
Tại \({t_2}\): \(\left\{ \begin{array}{l}{u_M} = 1,52mm\\{u_N} = + Amm\end{array} \right.\)
Ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}{\rm{cos}}\frac{\alpha }{2} = \frac{{1,52}}{A}\\{\rm{cos}}\alpha = \frac{{0,35}}{A} = {\rm{co}}{{\rm{s}}^2}\left( {\frac{\alpha }{2}} \right) - 1\end{array} \right.\\ \to \frac{{0,35}}{A} = 2.{(\frac{{1,52}}{A})^2} - 1\\ \to \frac{1}{A} = 0,5046 \to A = 1,98cm\end{array}\)
Suy ra
\(\begin{array}{l}cos\alpha = \frac{{0,35}}{A} = \frac{{0,35}}{{1,98}} = 0,1767\\ \to \alpha = 79,{82^0} \approx 0,44\pi \left( {rad} \right)\end{array}\)
Mặt khác, ta có: \(\alpha = \omega \Delta t \to \omega = \frac{\alpha }{{\Delta t}} = \frac{{0,44\pi }}{{0,11}} = 4\pi \left( {rad/s} \right)\)
=> Chu kì dao động: \(T = \frac{{2\pi }}{\omega } = \frac{{2\pi }}{{4\pi }} = 0,5s\)
Đáp án cần chọn là: a
Vật lý Lớp 12
