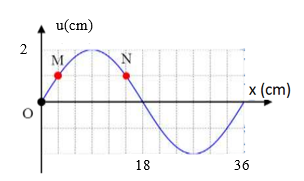
Một sóng ngang hình sin truyền trên một sợi dây dài. Hình vẽ bên là hình dạng của một đoạn dây tại một thời điểm xác định. Trong quá trình lan truyền sóng, khoảng cách lớn nhất giữa hai phần tử M và N có giá trị gần nhất với giá trị nào sau đây?
Phương pháp giải
+ Sử dụng phương pháp đọc đồ thị dao động sóng
+ Áp dụng biểu thức tính độ lệch pha giữa 2 phần tử: \(\Delta \varphi = \frac{{2\pi \Delta x}}{\lambda }\)
+ Áp dụng công thức tính khoảng cách giữa hai phần tử sóng: \(d = \sqrt {\Delta {x^2} + \Delta {u^2}} \)
Lời giải của Tự Học 365

Từ đồ thị, ta có: \(\lambda = 36cm\), \(\Delta x = 12cm\)
Độ lệch pha giữa 2 phần tử: \(\Delta \varphi = \frac{{2\pi \Delta x}}{\lambda } = \frac{{2\pi .12}}{{36}} = \frac{{2\pi }}{3}ra{\rm{d}}\)
Khoảng cách giữa hai phần tử sóng: \(d = \sqrt {\Delta {x^2} + \Delta {u^2}} \)
với \(\Delta x\) là không đổi, \(d\) lớn nhất khi \(\Delta u\) lớn nhất
Ta có:
\(\begin{array}{l}\Delta u = {\left( {{u_M} - {u_N}} \right)_{{\rm{max}}}}\\ = \sqrt {{A^2} + {A^2} - 2{\rm{AAcos}}\left( {\Delta \varphi } \right)} \\ = \sqrt {{A^2} + {A^2} - 2{\rm{AAcos}}\left( {\frac{{2\pi }}{3}} \right)} \\ = \sqrt 3 A = 2\sqrt 3 cm\end{array}\)
\( \to {d_{{\rm{max}}}} = \sqrt {\Delta {x^2} + \Delta {u_{{\rm{max}}}}^2} = \sqrt {{{12}^2} + {{\left( {2\sqrt 3 } \right)}^2}} \approx 12,5cm\)
Đáp án cần chọn là: c
Vật lý Lớp 12
