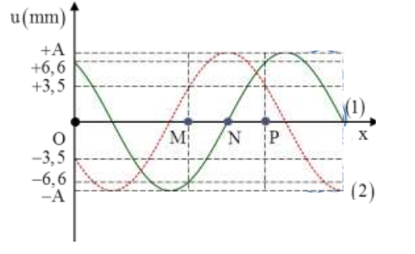
Trên một sợi dây đàn hồi có 3 điểm M, N và P là trung điểm của đoạn MB. Trên dây có sóng lan truyền từ M đến P với chu kì T (T > 0,5s). Hình vẽ bên mô tả hình dạng của sợi dây ở thời điểm t1 (nét liền) và t2 = t1 + 0,5s (nét đứt). M, N và P lần lượt là các vị trí cân bằng tương ứng. Lấy \(2\sqrt {11} = 6,6\) và coi biên độ sóng không đổi khi truyền đi. Tại thời điểm \({t_0} = {\rm{ }}{t_1} - \frac{1}{9}s\) vận tốc dao động của phần tử dây tại N là:
Phương pháp giải
+ Đọc đồ thị và áp dụng các công thức sóng cơ học.
+ Viết phương trình dao động sóng
+ Áp dụng công thức tính khoảng cách giữa hai phần tử sóng: \(d = \sqrt {{x^2} + \Delta {u^2}} \)
Lời giải của Tự Học 365
Từ đồ thị ta thấy rằng 2 thời điểm t1 và t2 vuông pha nhau, do đó:
\(\Delta \varphi = \omega \Delta t = \omega 0,5 = \left( {2k + 1} \right)\frac{\pi }{2} \to \omega = \left( {2k + 1} \right)\pi ra{\rm{d}}/s\) \({\left( {\frac{{{u_{1N}}}}{A}} \right)^2} + {\left( {\frac{{{u_{2N}}}}{A}} \right)^2} = 1 \to A = \sqrt {{u_{1N}}^2 + {u_{2N}}^2} = \sqrt {{{\left( {6,6} \right)}^2} + {{\left( { - 3,5} \right)}^2}} = 7,5mm\)
- Tại thời điểm t1 điểm N đang đi qua vị trí cân bằng theo chiều âm do vậy tốc độ của N sẽ là:
\({v_{{N_1}}} = \omega A = 7,5\pi \left( {2k + 1} \right)mm/s\)
- Vận tốc của N tại thời điểm
\({t_0} = {t_1} - \frac{1}{9}s\) là
\({v_{{N_0}}} = - {v_{{N_1}}}{\rm{cos}}\left( {2k + 1} \right)\frac{\pi }{9}mm/s\)
Với k = 1
\( \to {v_{{N_0}}} = - 7,5\pi .3{\rm{cos}}\frac{{3\pi }}{9}mm/s = - 35,3mm/s = - 3,53cm/s\)

Đáp án cần chọn là: b
Vật lý Lớp 12
