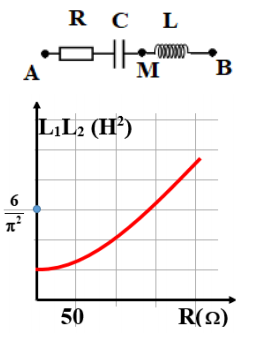
Đặt điện áp xoay chiều có tần số \(50Hz\) và giá trị hiệu dụng không đổi vào hai đầu mạch AB gồm biến trở \(R\), tụ điện \(C\) và cuộn cảm thuần có độ tự cảm \(L\) thay đổi được như hình vẽ. Khi \(L = L_1\) thì điện áp hiệu dụng ở hai đầu AM không phụ thuộc vào \(R\). Ứng với mỗi giá trị của \(R\), khi \(L = L_2\) thì điện áp hiệu dụng ở hai đầu cuộn cảm đạt giá trị cực đại. Hình bên là đồ thị biểu diễn sự phụ thuộc của tích \(L_1L _2\) theo \(R\). Để công suất tiêu thụ của mạch ứng với mỗi \(R\) đạt cực đại thì giá trị của \(L\) là
Phương pháp giải
Cảm kháng ZL = ωL
Tổng trở mạch RLC là \(Z = \sqrt {{R^2} + {{({Z_L} - {Z_C})}^2}} \)
Định luật Ôm cho đoạn mạch : I = U/Z
Mạch RLC có L thay đổi để UL max thì \({Z_L} = \dfrac{{{R^2} + Z_C^2}}{{{Z_C}}}\)
L thay đổi để công suất mạch cực đại thì mạch xảy ra cộng hưởng, khi đó ZL = ZC
Lời giải của Tự Học 365
+ L thay đổi để UAM = \(\dfrac{U}{{\sqrt {{R^2} + Z_{LC}^2} }}.\sqrt {{R^2} + Z_C^2} \) không phụ thuộc vào R nên
\({R^2} + Z_C^2 = {R^2} + Z_{LC}^2 \to Z_C^2 = {({Z_L} - {Z_C})^2} \Rightarrow {Z_{L1}} = 2{Z_C}\) (1)
+ L thay đổi để UL max nên \({Z_{L2}} = \dfrac{{{R^2} + Z_C^2}}{{{Z_C}}}\) (2)
+ Nhìn vào đồ thị ta thấy khi R = 100Ω thì \({L_1}{L_2} = \dfrac{4}{{{\pi ^2}}} \Rightarrow {Z_{L1}}{Z_{L2}} = \dfrac{4}{{{\pi ^2}}}.{\omega ^2} = 40000\) (3)
Từ (1), (2), (3) ta được ZC= 100Ω
Để công suất tiêu tụ của mạch cực đại thì ZL = ZC = 100Ω \( \Rightarrow L = \dfrac{1}{\pi }(H)\)
Đáp án cần chọn là: d
Vật lý Lớp 12
