Một vật dao động điều hòa trên trục Ox theo phương trình \(x = A\cos \left( {\dfrac{\pi }{3}t + \varphi } \right)\) ( t tính bằng giây). Trong ba khoảng thời gian theo thứ tự liên tiếp là \(\Delta t = 1s;\Delta {t_2} = \Delta {t_3} = 2s\) thì quãng đường chuyển động của vật lần lượt là \({S_1} = 5cm;{S_2} = 15cm\) và quãng đường S3. Quãng đường S3 gần nhất với giá trị nào sau đây:
Phương pháp giải
Sử dụng vòng tròn lượng giác trong dao động điều hòa
Lời giải của Tự Học 365
Ta có:
\(T = \dfrac{{2\pi }}{\omega } = 6s \\\to \left\{ \begin{array}{l}\Delta {t_1} + \Delta {t_2} = \dfrac{T}{2}\\{S_1} + {S_2} = 2A = 20cm\end{array} \right. \\\to A = 10cm \\\to \left\{ \begin{array}{l}\Delta {t_1} = 1s = \dfrac{T}{6}\\{S_1} = 5cm = \dfrac{A}{2}\end{array} \right.\)
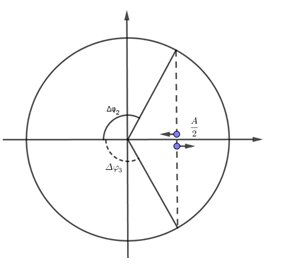
Suy ra vật xuất phát từ 2 biên ( giá sử từ biên dương) , vậy \(\Delta {t_2} = \Delta {t_3} = 2s = \dfrac{T}{3} \to {S_2} = {S_3} = 15cm\)
Đáp án cần chọn là: b
Vật lý Lớp 12
