Một vật dao động điều hòa với tần số bằng \(5Hz\). Thời gian ngắn nhất để vật đi từ vị trí có li độ \({x_1} = - 0,5A\) đến vị trí có li độ \({x_2} = + 0,5A\) là:
Phương pháp giải
+ Sử dụng biểu thức tính chu kì dao động của vật: \(T = \dfrac{1}{f}\)
+ Sử dụng vòng tròn lượng giác
Lời giải của Tự Học 365
+ Chu kì dao động của vật: \(T = \dfrac{1}{f} = \dfrac{1}{5}s\)
+ Vật đi từ vị trí có li độ \({x_1} = - 0,5A \to {x_2} = 0,5A\)
Vẽ trên vòng tròn lượng giác ta được:
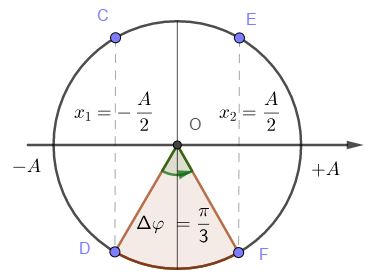
Thời gian ngắn nhất để vật đi từ vị trí có li độ \({x_1} = - \dfrac{A}{2} \to {x_2} = \dfrac{A}{2}\) là: \(\Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{\pi }{3}}}{{\dfrac{{2\pi }}{T}}} = \dfrac{T}{6} = \dfrac{{\dfrac{1}{5}}}{6} = \dfrac{1}{{30}}s\)
Đáp án cần chọn là: c
Vật lý Lớp 12
