Vật đang dao động điều hòa dọc theo đường thẳng. Một điểm M nằm trên đường thẳng đó, phía ngoài khoảng chuyển động của vật, tại thời điểm t thì vật xa điểm M nhất, sau đó một khoảng thời gian ngắn nhất là $\Delta t$ thì vật gần điểm M nhất. Vận đến li độ \(x = \dfrac{A}{2}\) vào thời điểm:
Phương pháp giải
Sử dụng trục thời gian suy ra từ vòng tròn.
Lời giải của Tự Học 365
Giả sử điểm M nằm phía ngoài gần biên dương
+ Ta có, tại thời điểm \(t\) vật xa điểm M nhất => đang ở biên âm
Tại \(t + \Delta t\): vật gần M nhất => đang ở biên dương
=> \(\Delta t\) là khoảng thời gian vật đi từ biên âm đến biên dương
\( \to \Delta t = \dfrac{T}{2} \to T = 2\Delta t\)
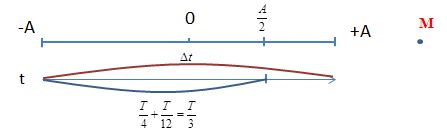
=> Vận đến li độ \(x = \dfrac{A}{2}\) vào thời điểm: \(t + \dfrac{T}{3} = t + \dfrac{{2\Delta t}}{3}\)
Đáp án cần chọn là: d
Vật lý Lớp 12
