Một vật dao động điều hoà với phương trình \(x = Acos\left( {\omega t + \dfrac{\pi }{6}} \right)\). Biết quãng đường vật đi được trong thời gian \(1s\) tính từ thời điểm gốc là \(2A\) và trong \(\dfrac{2}{3}s\) là \(12cm\). Giá trị của \(A\) và \(f\) là:
Phương pháp giải
+ Quãng đường vật đi được \(2A\) trong khoảng thời gian \(\dfrac{T}{2}\)
+ Áp dụng công tính tần số: \(f = \dfrac{1}{T}\)
+ Xác định vị trí của vật tại thời điểm ban đầu \(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\varphi \\v = - A\omega \sin \varphi \end{array} \right.\)
+ Sử dụng trục thời gian suy ra từ vòng tròn, công thức \(\Delta \varphi = \omega \Delta t\)
Lời giải của Tự Học 365
+ Ta có khoảng thời gian vật đi được quãng đường \(2A\) là \(\dfrac{T}{2}\)
\( \to \dfrac{T}{2} = 1{\rm{s}} \to T = 2{\rm{s}}\)
+ Tần số của dao động: \(f = \dfrac{1}{T} = \dfrac{1}{2} = 0,5Hz\)
+ Tại \(t{\rm{ }} = {\rm{ }}0\): \(\left\{ \begin{array}{l}{x_0} = Ac{\rm{os}}\dfrac{\pi }{6}\\v = - A\omega \sin \dfrac{\pi }{6}\end{array} \right. \to \left\{ \begin{array}{l}{x_0} = \dfrac{{A\sqrt 3 }}{2}\\v < 0\end{array} \right.\)
+ Trong khoảng thời gian \(\Delta t = \dfrac{2}{3}s = \dfrac{T}{3}\) từ thời điểm gốc vật đi được quãng đường \(S = 12cm\)
Góc quét: \(\Delta \varphi = \omega \Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{3} = \dfrac{{2\pi }}{3}\)
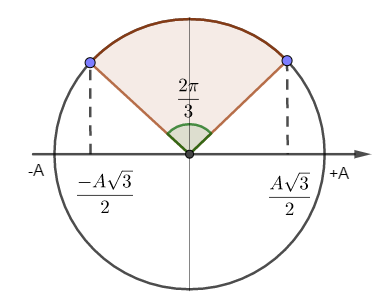
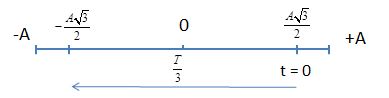
Ta có: \(S = \dfrac{{A\sqrt 3 }}{2} + \left| { - \dfrac{{A\sqrt 3 }}{2}} \right| = A\sqrt 3 = 12cm \to A = 4\sqrt 3 cm\)
Đáp án cần chọn là: a
Vật lý Lớp 12
