Một vật dao động điều hòa có phương trình $x = 5c{\rm{os}}\left( {4\pi t + \frac{\pi }{3}} \right)\left( {cm,s} \right)$. Tốc độ trung bình của vật trong khoảng thời gian tính từ lúc bắt đầu khảo sát dao động đến thời điểm vật đi qua vị trí cân bằng theo chiều dương lần thứ nhất là:
Phương pháp giải
+ Sử dụng công thức tính chu kì dao động: \(T = \dfrac{{2\pi }}{\omega }\)
+ Xác định vị trí tại $t = 0 (x,v)$
+ Xác định quãng đường vật đi được
+ Sử dụng công thức tính tốc độ trung bình: \({v_{tb}} = \dfrac{S}{t}\)
Lời giải của Tự Học 365
Chu kì \(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{4\pi }} = 0,5{\rm{s}}\)
$t = 0$: \(\left\{ \begin{array}{l}x = 2,5\\v < 0\end{array} \right.\)
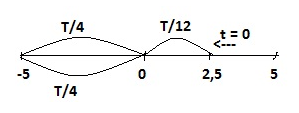
Theo hình vẽ:
\(\Delta t = \dfrac{T}{{12}} + \dfrac{T}{4} + \dfrac{T}{4} = \dfrac{{7T}}{{12}} = \dfrac{7}{{24}}s\)
$S = 2,5+ 5.2 = 12,5 cm$
Tốc độ trung bình:
\({v_{tb}} = \dfrac{S}{t} = \dfrac{{12,5}}{{\dfrac{7}{{24}}}} = 42,86cm/s\)
Đáp án cần chọn là: b
Vật lý Lớp 12
