Vật dao động điều hoà theo phương trình $x = 5\cos \left( {2\pi t - \frac{\pi }{4}} \right)cm$. Tốc độ trung bình của vật đi được trong khoảng thời gian từ ${t_1} = 1s$ đến ${t_2} = 4,625s$ là:
Phương pháp giải
+ Áp dụng công thức tính chu kì dao động: \(T = \dfrac{{2\pi }}{\omega }\)
+ Xác định (x,v) tại thời điểm t bằng cách thay t vào phương trình
+ Sử dụng vòng tròn lượng giác được suy ra từ vòng tròn
+ Áp dụng công thức tính tốc độ trung bình: \({v_{tb}} = \dfrac{S}{{\Delta t}}\)
Lời giải của Tự Học 365
Chu kì dao động:
\(T = \dfrac{{2\pi }}{\omega } = \dfrac{{2\pi }}{{2\pi }} = 1{\rm{s}}\)
Tại t = 1s:
\(\left\{ \begin{array}{l}x = 5c{\rm{os}}\left( {2\pi .1 - \dfrac{\pi }{4}} \right) = 2,5\sqrt 2 \\v = - A\omega \sin \left( {2\pi .1 - \dfrac{\pi }{4}} \right) > 0\end{array} \right.\)
Tại t = 4,625s:
\(\left\{ \begin{array}{l}x = 5c{\rm{os}}\left( {2\pi .4,625 - \dfrac{\pi }{4}} \right) = - 5\\v = - A\omega \sin \left( {2\pi .4,625 - \dfrac{\pi }{4}} \right) = 0\end{array} \right.\)
Khoảng thời gian:
\(\Delta t = 3,625{\rm{s}} = 3T + \dfrac{T}{2} + \dfrac{T}{8}\)
Quãng đường S trong khoảng thời gian đó:
\(S = 3.4A + 2A + \left( {A - \dfrac{{A\sqrt 2 }}{2}} \right) = 15A - \dfrac{{A\sqrt 2 }}{2} = 71,464cm\)
Tốc độ trung bình vật đi được trong khoảng thời gian đó là:
\({v_{tb}} = \dfrac{S}{{\Delta t}} = \dfrac{{71,464}}{{3,625}} = 19,71cm/s\)
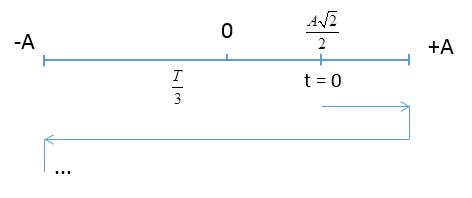
Đáp án cần chọn là: d
Vật lý Lớp 12
