Một vật dao động điều hòa theo phương trình \(x = 4c{\rm{os}}\left( {10\pi t - \dfrac{\pi }{4}} \right)cm\) (t tính bằng giây). Tìm quãng đường vật đi được kể từ lúc bắt đầu dao động đến khi vật có tốc độ \(0,2\pi \sqrt 3 m/s\) lần thứ hai?
Phương pháp giải
+ Sử dụng phương pháp đại số xác định quãng đường vật đi được từ li độ x1 đến x2
+ Sử dụng hệ thức độc lập:
\({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}}\)
Lời giải của Tự Học 365
Tại $t=0$:
\(\left\{ \begin{array}{l}{x_0} = 4c{\rm{os}}\left( {\frac{-\pi }{4}} \right) = 2\sqrt 2 cm\\v = - 40\pi \sin \left( {\frac{-\pi }{4}} \right) = 20\pi \sqrt 2 > 0\end{array} \right.\)
Tại $v=$\(0,2\pi \sqrt 3 m/s\):
\(x = \pm \sqrt {{A^2} - \frac{{{v^2}}}{{{\omega ^2}}}} = \pm \sqrt {0,{{04}^2} - \frac{{{{\left( {0,2\pi \sqrt 3 } \right)}^2}}}{{{{\left( {10\pi } \right)}^2}}}} = \pm 0,02m = \pm 2cm\)
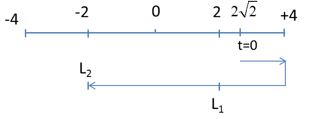
=> Quãng đường vật đi được: \(S = {\rm{ }}(4 - 2\sqrt 2 ) + 4 + 2 = 10 - 2\sqrt 2 cm\)
Đáp án cần chọn là: c
Vật lý Lớp 12
