Một mạch dao động \(LC\) có \(L{\rm{ }} = {\rm{ }}2mH,{\rm{ }}C = 8pF\) , lấy \({\pi ^2} = 10\). Thời gian từ lúc tụ bắt đầu phóng điện đến lúc có năng lượng điện trường bằng ba lần năng lượng từ trường là:
Phương pháp giải
+ Sử dụng biểu thức tính chu kì dao động : \(T = 2\pi \sqrt {LC} \)
+ Vận dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \frac{1}{2}C{U_0}^2 = \frac{{{Q_0}^2}}{{2C}} = \frac{{LI{{_0^{}}^2}}}{2}\)
+ Vận dụng biểu thức: \(\Delta \varphi = \omega \Delta t\)
Lời giải của Tự Học 365
Ta có: \(T = 2\pi \sqrt {LC} = 2\pi \sqrt {{{2.10}^{ - 3}}{{.8.10}^{ - 12}}} = {8.10^{ - 7}}s\)
Đề cho: \({W_C}{\rm{ }} = 3{W_L} \to {W_L} = \frac{{{W_C}}}{3}\)
\(\begin{array}{l}{\rm{W}} = {{\rm{W}}_C} + {{\rm{W}}_L} = {{\rm{W}}_C} + \frac{{{{\rm{W}}_C}}}{3} = \frac{4}{3}{{\rm{W}}_C}\\ \leftrightarrow \frac{{q_0^2}}{{2C}} = \frac{4}{3}\frac{{{q^2}}}{{2C}}\\ \to q = \frac{{\sqrt 3 }}{2}{q_0}\end{array}\)
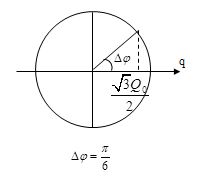
Hình vẽ cho ta góc quét : \(\Delta \varphi = \frac{\pi }{6}\)
Mặt khác, ta có : \(\Delta \varphi = \omega \Delta t \to \Delta t = \frac{{\Delta \varphi }}{\omega } = \frac{{\frac{\pi }{6}}}{{\frac{{2\pi }}{T}}} = \frac{T}{{12}}\)
\(\Delta t = \frac{T}{{12}} = \frac{{{{8.10}^{ - 7}}}}{{12}} = \frac{2}{3}{10^{ - 7}} = \frac{1}{{15}}{10^{ - 6}}s\)
Đáp án cần chọn là: d
Vật lý Lớp 12
