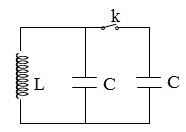
Mạch dao động điện từ gồm cuộn cảm và một bộ hai tụ điện có cùng điện dung \(C = 2,5\mu F\) mắc song song. Trong mạch có dao động điện từ tự do, hiệu điện thế cực đại giữa hai bản tụ điện là \({U_0} = 12V\). Tại thời điểm hiệu điện thế hai đầu cuộn cảm \({u_L} = 6V\) thì một tụ điện bị bong ra vì đứt dây nối. Tính năng lượng cực đại trong cuộn cảm sau đó:
Phương pháp giải
Sử dụng biểu thức tính năng lượng của mạch dao động: \({\rm{W}} = {{\rm{W}}_L} + {{\rm{W}}_C} = \dfrac{1}{2}C{U_0}^2 = \dfrac{{{Q_0}^2}}{{2C}} = \dfrac{{LI{{_0^{}}^2}}}{2}\)
Lời giải của Tự Học 365
+ Năng lượng ban đầu của mạch dao động:
\({W_0} = \dfrac{{{C_b}U_0^2}}{2} = \dfrac{{2CU_0^2}}{2} = C{U_0}^2 = 2,{5.10^{ - 6}}144{\rm{ }} = {\rm{ }}{360.10^{ - 6}}J = {\rm{ }}0,360{\rm{ }}mJ\)
+ Năng lượng của cuộn cảm khi \({u_L} = {\rm{ }}6V\): \( \to {u_C} = {u_L}\)
\({W_C} = \dfrac{{2Cu_L^2}}{2} = {\rm{ }}C{u_L}^2 = {90.10^{ - 6}}J = 0,090mJ\)
\({W_L} = {\rm{ }}{W_0}-{\rm{ }}{W_C} = {\rm{ }}0,360{\rm{ }}-{\rm{ }}0,090{\rm{ }} = {\rm{ }}0,270{\rm{ }}mJ\)
+ Khi một tụ bị hỏng, năng lượng của mạch:
\(W{\rm{ }} = {\rm{ }}{W_L} + \dfrac{{{W_C}}}{2} = 0,270{\rm{ }} + {\rm{ }}0,045{\rm{ }} = {\rm{ }}0,315{\rm{ }}mJ\)
Do đó: \({W_{Lmax}} = {\rm{ }}W{\rm{ }} = {\rm{ }}0,315{\rm{ }}mJ\)
Đáp án cần chọn là: c
Vật lý Lớp 12
