Theo mẫu nguyên tử Bo, mức năng lượng của trạng thái dừng thứ n của nguyên tử Hidro được xác định theo công thức \({E_n} = - \dfrac{{13,6}}{{{n^2}}}\left( {eV} \right);\left( {n = 1,2,3...} \right)\) Gọi R1 là bán kính quỹ đạo của e khi nguyên tử Hidro ở tạng thái dừng L. Khi nguyên tử ở trạng thái dừng ứng với bán kính bằng 9R1 thì tỷ số bước sóng lớn nhất và bước sóng nhỏ nhất của photon mà nguyên tử Hidro có thể phát xạ là:
Phương pháp giải
Áp dụng công thức xác định mức năng lượng của photon: \({E_n} = - \dfrac{{13,6}}{{{n^2}}}\left( {eV} \right);\left( {n = 1,2,3...} \right)\)
Lời giải của Tự Học 365
R1 là bán kính quỹ đạo e ứng với trạng thái dừng L vậy \({r_1} = {2^2}{r_0}\)
Khi bán kính quỹ đạo là 9R1 ta có \(r = 9{r_1} = 9.4{r_0} = 36{r_0} = > n = 6\) ứng với trạng thái dừng P
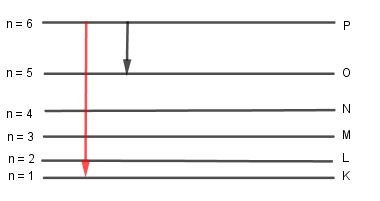
Bước sóng lớn nhất mà photon này có thể phát xạ ra khi nó chuyển mức năng lượng từ trạng thái P về trạng thái K là \(E = {E_P} - {E_0} = \dfrac{{{E_0}}}{{{6^2}}} - {E_0} = \dfrac{{35}}{{36}}{E_0} = \dfrac{{hc}}{{{\lambda _{max}}}} = > {\lambda _{max}} = \dfrac{{hc}}{{\dfrac{{35}}{{36}}{E_0}}}\)
Bước sóng ngắn nhất photon này có thể phát xạ ra khi nó chuyển mức năng lượng từ trạng thái P về trạng thái O là \(E = {E_P} - {E_O} = \dfrac{{{E_0}}}{{{6^2}}} - \dfrac{{{E_0}}}{5} = \dfrac{{11}}{{900}}{E_0} = \dfrac{{hc}}{{{\lambda _{\min }}}} = > {\lambda _{\min }} = \dfrac{{hc}}{{\dfrac{{11}}{{900}}{E_0}}}\)
Tỷ số giữa bước sóng ngắn lớn nhất và dài nhất là \(\dfrac{{{\lambda _{\min }}}}{{{\lambda _{max}}}} = \dfrac{{\dfrac{{hc}}{{\dfrac{{35}}{{36}}{E_0}}}}}{{\dfrac{{hc}}{{\dfrac{{11}}{{900}}{E_0}}}}} = \dfrac{{35}}{{36}}.\dfrac{{900}}{{11}} = \dfrac{{875}}{{11}}\)
Đáp án cần chọn là: d
Vật lý Lớp 12
