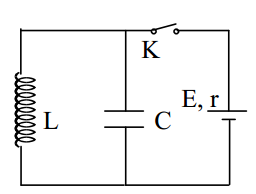
Cho mạch điện như hình vẽ bên, nguồn điện một chiều có suất điện động \(E\) không đổi và điện trở trong \(r\),cuộn dây thuần cảm \(L\) và tụ điện có điện dung \(C{\rm{ }} = {\rm{ }}{2,5.10^7}F\). Ban đầu khóa \(K\) mở, tụ chưa tích điện. Đóng khóa \(K\), khi mạch ổn định thì mở khóa \(K\). Lúc này trong mạch có dao động điện từ tự do với chu kì bằng \(\pi {.10^{ - 6}}s\) và hiệu điện thế cực đại trên tụ bằng \(2E\) .Giá trị của \(r\) bằng:
Phương pháp giải
+ Biểu thức định luật Ôm: \(I = \dfrac{E}{r}\)
+ Năng lượng điện từ trong mạch: \(W = \dfrac{{L{I_0}^2}}{2} = \dfrac{{C{U_0}^2}}{2}\)
Lời giải của Tự Học 365
+ Khi \(K\) đóng, tụ điện được tích điện đến hiệu điện thế\({U_0} = {\rm{ }}2E\), dòng điện trong mạch lúc này là: \({I_0} = \dfrac{E}{r}\left( 1 \right)\)
+ Khi K mở, mạch LC dao động điện từ tự do, ta có:
\(\dfrac{1}{2}CU_0^2 = \dfrac{1}{2}LI_0^2 \Leftrightarrow CU_0^2 = LI_0^2 \Leftrightarrow {C^2}U_0^2 = LCI_0^2 = \dfrac{{{T^2}}}{{4{\pi ^2}}}I_0^2 \Leftrightarrow {I_0} = \dfrac{{2\pi C{U_0}}}{T}\left( 2 \right)\)
Từ (1) và (2) ta có : \(\dfrac{E}{r} = \dfrac{{2\pi C{U_0}}}{T} = \dfrac{{2\pi C.2E}}{T} \Rightarrow r = \dfrac{T}{{4\pi C}} = \dfrac{{\pi {{.10}^{ - 6}}}}{{4\pi {{.2,5.10}^{ - 7}}}} = 1\Omega \)
Đáp án cần chọn là: c
Vật lý Lớp 12
