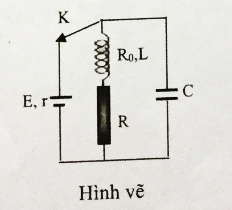
Cho mạch điện như hình vẽ, nguồn có suất điện động \(E = 24V,r = 1\Omega \) , tụ điện có điện dung \(C = 100\mu F\), cuộn dây có hệ số tự cảm \(L = 0,2H\) và điện trở \({R_0} = 5\Omega \), điện trở \(R = 18\Omega \). Ban đầu khóa k đóng, khi trạng thái trong mạch đã ổn định người ta ngắt khóa k. Nhiệt lượng tỏa ra trên điện trở \(R\) trong thời gian từ khi ngắt khóa k đến khi dao động mạch tắt hoàn toàn.
Phương pháp giải
Sử dụng lí thuyết về dao động điện từ trong mạch LC kết hợp với kiến thức về định luật Ôm cho toàn mạch
+ Biểu thức định luật Ôm: \(I = \frac{E}{{{R_b} + r}}\)
+ Hiệu điện thế hai đầu nguồn điện: \(U = E - {\rm{Ir}}\)
+ Năng lượng điện từ: \({\rm{W}} = {{\rm{W}}_C} + {{\rm{W}}_L} = \frac{1}{2}C{U^2} + \frac{1}{2}L{I^2}\)
Lời giải của Tự Học 365
+ Khi khóa K đóng
Cường độ dòng điện chạy trong mạch : \(I = \frac{E}{{R + {R_0} + r}} = \frac{{24}}{{18 + 5 + 1}} = 1(A)\)
Hiệu điện thế hai đầu nguồn điện, cũng chính là hiệu điện thế hai đầu tụ: \(U = E - {\rm{Ir}} = 24 - 1 = 23(V)\)
+ Khi ngắt khóa K thì trong mạch có dao động điện từ tắt dần
Năng lượng điện từ ban đầu trong mạch dao động là:
\({\rm{W}} = {{\rm{W}}_C} + {{\rm{W}}_L} = \frac{1}{2}C{U^2} + \frac{1}{2}L{I^2} = \frac{1}{2}{.100.10^{ - 6}}{.23^2} + \frac{1}{2}{0,2.1^2} = 0,12645(J)\)
Khi dao động trong mạch tắt hoàn toàn thì năng lượng điện từ của mạch chuyển hóa hết thành nhiệt tỏa ra trên hai điện trở R và R0
Ta có: \(\left\{ \begin{array}{l}{Q_R} + {Q_{{R_0}}} = {\rm{W = 0}}{\rm{,12645}}\\\frac{{{Q_R}}}{{{Q_{{R_0}}}}} = \frac{R}{{{R_0}}} = \frac{{18}}{5}\end{array} \right. = > \left\{ \begin{array}{l}{Q_R} = 0,09896(J) = 98,96(mJ)\\{Q_{{R_0}}} = 0,02749(J)\end{array} \right.\)
Đáp án cần chọn là: b
Vật lý Lớp 12
