Cho mạch điện như hình vẽ:
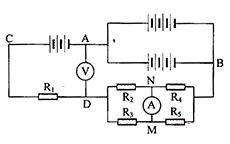
Phương pháp giải
+ Áp dụng biểu thức xác định suất điện động bộ nguồn khi mắc hỗn hợp đối xứng: \({E_b} = {\rm{ }}m.E\).
+ Áp dụng biểu thức xác định suất điện động bộ nguồn mắc nối tiếp
+ Áp dụng biểu thức xác định điện trở trong của bộ nguồn khi mắc hỗn hợp đối xứng: \(\;{r_b} = \dfrac{{m.r}}{n}\)
+ Áp dụng biểu thức xác định điện trở trong của bộ nguồn mắc nối tiếp
+ Áp dụng định luật Ôm cho toàn mạch
Lời giải của Tự Học 365
Ta có:
+ Suất điện động của bộ nguồn: \({E_b} = 3E + 4E = 7E = 7.2 = 14V\)
+ Điện trở trong của bộ nguồn là: \({r_b} = 3r + \dfrac{4}{2}r = 5r = 5\Omega \)
+ Vì vôn kế có điện trở rất lớn nên dòng điện không qua nhánh chứa vôn kế.
Ampe kế có điện trở rất nhỏ nên hai điểm M và N cùng điện thế, chập M và N mạch được vẽ lại như hình:

Ta thấy, mạch gồm: \({R_1}nt\left[ {{R_2}//{R_3}} \right]nt\left[ {{R_4}//{R_5}} \right]\)
\({R_{23}} = \dfrac{{{R_2}{R_3}}}{{{R_2} + {R_3}}} = \dfrac{{8.8}}{{8 + 8}} = 4\Omega \)
\({R_{45}} = \dfrac{{{R_4}{R_5}}}{{{R_4} + {R_5}}} = \dfrac{{20.30}}{{20 + 30}} = 12\Omega \)
Tổng trở của mạch ngoài: \({R_N} = {R_1} + {R_{23}} + {R_{45}} = 7 + 4 + 12 = 23\Omega \)
+ Cường độ dòng điện trong mạch chính: \(I = \dfrac{{{E_b}}}{{{R_N} + {r_b}}} = \dfrac{{14}}{{23 + 5}} = 0,5A\)
+ Ta có: \({I_1} = {I_{23}} = {I_{45}} = 0,5A\)
Lại có: \(\left\{ \begin{array}{l}{U_{23}} = {I_{23}}.{R_{23}} = 2V \Rightarrow {U_2} = {U_3} = 2V\\{U_{45}} = {I_{45}}.{R_{45}} = 6V \Rightarrow {U_4} = {U_5} = 6V\end{array} \right.\)
+ Vì \({R_2} = {R_3} \Rightarrow I{_2} = {I_3} = \dfrac{{{I_{23}}}}{2} = 0,25A\)
Ta có: \({I_4} = \dfrac{{{U_4}}}{{{R_4}}} = \dfrac{6}{{20}} = 0,3A\) , \({I_5} = {I_{45}} - {I_4} = 0,5 - 0,3 = 0,2A\)
+ Từ mạch gốc tại N ta thấy: \({I_2} = 0,25 < {I_4} = 0,3A\) nên dòng qua ampe kế phải có chiều từ M đến N.
Số chỉ của ampe kế là: \({I_A} = {I_4} - {I_2} = 0,3 - 0,25 = 0,05A\)
Đáp án cần chọn là: a
Vật lý Lớp 12
