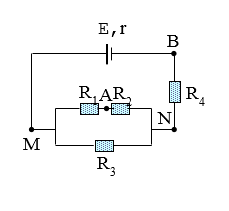
Cho mạch điện có sơ đồ như hình vẽ:
Trong đó: E = 1,2 V, r = 0,1\(\Omega \), R1 = R3 = 2\(\Omega \). R2 = R4 = 4\(\Omega \). Hiệu điện thế giữa hai điểm A, B là:
Phương pháp giải
+ Áp dụng biểu thức xác định điện trở tương đương của mạch
+ Áp dụng biểu thức định luật Ôm với toàn mạch
Lời giải của Tự Học 365
Ta có:
+ Mạch ngoài gồm: R4 nt (R3// (R1 nt R2))
R12 = R1 + R2 = 2 + 4 = 6$\Omega $
- Điện trở đoạn MN là:
\({R_{MN}} = \frac{{{R_3}{R_{12}}}}{{{R_3} + {R_{12}}}}{\rm{ = }}1,5\Omega .\)
- Điện trở tương đương của mạch ngoài: R = R4 +RMN = 4 + 1,5 = 5,5$\Omega $
- Dòng điện qua mạch chính:
\(I{\rm{ }} = \frac{E}{{R + r}} = \frac{{1,2}}{{5,5 + 0,1}} = \frac{3}{{14}}{\rm{ }}A.\)
- Hiệu điện thế giữa M, N :
\({U_{MN}} = I.{R_{MN}} = \frac{3}{{14}}.1,5 = \frac{9}{{28}}V\) .
- Cường độ dòng điện qua R2:
\({I_2} = \frac{{{U_{MN}}}}{{{R_1} + {R_2}}} = \frac{{\frac{9}{{28}}}}{6} = \frac{3}{{56}}A\)
- Hiệu điện thế giữa A,N:
\({U_{AN}} = {I_2}.{R_2} = \frac{3}{{56}}.4 = \frac{3}{{14}}V\)
- Hiệu điện thế giữa N và B:
\({U_{NB}} = I.{R_4} = \frac{3}{{14}}.4 = \frac{6}{7}V\) .
- Hiệu điện thế giữa A và B :
\({U_{AB}} = {\rm{ }}{U_{AN}} + {\rm{ }}{U_{NB}} = \frac{3}{{14}} + \frac{6}{7} = 1,07V\)
Đáp án cần chọn là: c
Vật lý Lớp 12
