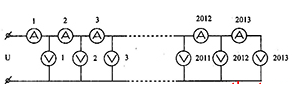
Cho \(2013\) ampe kế không lý tưởng; \(2013\) vôn kế giống nhau không lí tưởng mắc như hình, ampe kế \({A_1}\) chỉ \(2A\); ampe kế \({A_2}\) chỉ \(1,5A\), vôn kế \({V_1}\) chỉ \(503,5V\). Hãy tìm tổng số chỉ của \(2013\) vôn kế trong mạch.
Phương pháp giải
Vận dụng biểu thức định luật ôm: \(I = \dfrac{U}{R}\)
Lời giải của Tự Học 365
+ Từ mạch điện, ta có: dòng điện qua vôn kế \({V_1}\) là: \(I = {I_{{A_1}}} - {I_{{A_2}}} = 2 - 1,5 = 0,5A\)
+ Điện trở của mỗi vôn kế: \({R_V} = \dfrac{{{U_1}}}{{{I_1}}} = \dfrac{{503,5}}{{0,5}} = 1007\Omega \) (1)
+ Từ mạch điện ta có: \(\left\{ \begin{array}{l}{I_{{A_1}}} = {I_{{A_2}}} + \dfrac{{{U_1}}}{{{R_V}}}\\{I_{{A_2}}} = {I_{{A_3}}} + \dfrac{{{U_2}}}{{{R_V}}}\\.......\\{I_{{A_{2012}}}} = {I_{{A_{2013}}}} + \dfrac{{{U_{2012}}}}{{{R_V}}}\\{I_{{A_{2013}}}} = {I_{V2013}}\end{array} \right.\)
+ Cộng vế với vế của các phương trình trên, ta có:
\({I_{{A_1}}} = {I_{V2013}} + \dfrac{{{U_{2012}}}}{{{R_V}}} + \dfrac{{{U_{2011}}}}{{{R_V}}} + ... + \dfrac{{{U_2}}}{{{R_V}}} + \dfrac{{{U_1}}}{{{R_V}}}\)
\( \Rightarrow {I_{{A_1}}}{R_V} = {I_{V2013}}{R_V} + {U_{2012}} + {U_{2011}} + ... + {U_2} + {U_1}\)
\( \Rightarrow {I_{{A_1}}}{R_V} = {U_{2013}} + {U_{2012}} + {U_{2011}} + ... + {U_2} + {U_1}\) (2)
+ Từ (1) và (2), ta suy ra:
\({U_1} + {U_2} + {U_3} + ... + {U_{2013}} = {I_{{A_1}}}{R_V} = 2.1007 = 2014V\)
Đáp án cần chọn là: c
Vật lý Lớp 12
