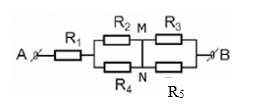
Cho mạch điện như hình vẽ.
R1 = 2,4$\Omega $, R2 = 14$\Omega $, R3 = 4$\Omega $, R4 = R5 = 6$\Omega $, I3 = 2A.
Hiệu điện thế giữa hai đầu đoạn mạch UAB là?
Phương pháp giải
+ Áp dụng biểu thức xác định điện trở trong mạch nối tiếp: R = R1 + R2 + .... + Rn
+ Áp dụng biểu thức xác định điện trở trong mạch song song: \(\frac{1}{R} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + ... + \frac{1}{{{R_n}}}\)
+ Áp dụng biểu thức cường độ dòng điện trong mạch nối tiếp và song song (Xem phần II + III)
+ Áp dụng biểu thức định luật Ôm cho đoạn mạch chỉ có điện trở: \(I = \frac{U}{R}\)
Lời giải của Tự Học 365
Ta nhận thấy giữa hai điểm M, N không có điện trở => ta có thể chập lại thành một điểm khi đó mạch trở thành:
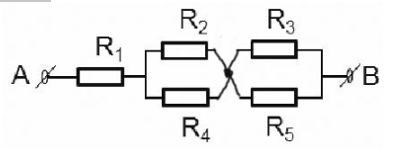
=> Đoạn mạch gồm: R1 nt (R2 // R4) nt (R3 // R5)
\(\frac{1}{{{R_{24}}}} = \frac{1}{{{R_2}}} + \frac{1}{{{R_4}}} \to {R_{24}} = \frac{{{R_2}{R_4}}}{{{R_2} + {R_4}}} = \frac{{14.6}}{{14 + 6}} = 4,2\Omega \)
\(\frac{1}{{{R_{35}}}} = \frac{1}{{{R_3}}} + \frac{1}{{{R_5}}} \to {R_{35}} = \frac{{{R_3}{R_5}}}{{{R_3} + {R_5}}} = \frac{{4.6}}{{4 + 6}} = 2,4\Omega \)
\(R = {R_1} + {R_{24}} + {R_{35}} = 2,4 + 4,2 + 2,4 = 9\Omega \)
Ta có: U3 = U5 = U35 = I3.R3 = 2.4 = 8V
\( \to {I_5} = \frac{{{U_5}}}{{{R_5}}} = \frac{8}{6} = \frac{4}{3}A \to {I_{35}} = {I_3} + {I_5} = 2 + \frac{4}{3} = \frac{{10}}{3}A\)
\(I = {I_1} = {I_{24}} = {I_{35}} = \frac{{10}}{3}A \to {U_{AB}} = IR = \frac{{10}}{3}.9 = 30V\)
Đáp án cần chọn là: a
Vật lý Lớp 12
