Toán11
Danh sách câu hỏi
-
[ Một câu lạc bộ có 25 thành viên. Số cách chọn một ban quản lí gồm 1 chủ tịch 1 phó chủ tịch và một - Tự Học 365] Một câu lạc bộ có 25 thành viên. Số cách chọn một ban quản lí gồm 1 chủ tịch, 1 phó chủ tịch và một thư ký là:
-
[Trong khai triển ( 3x^2 - y )^10 hệ số của số hạng chính giữa là: - Tự Học 365] Trong khai triển \({\left( {3{x^2} - y} \right)^{10}}\), hệ số của số hạng chính giữa là:
-
[Từ các chữ số 123456789 có thể lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau và lớ - Tự Học 365] Từ các chữ số \(1,2,3,4,5,6,7,8,9\) có thể lập được bao nhiêu số tự nhiên gồm năm chữ số đôi một khác nhau và lớn hơn \(50000\).
-
[Trong khai triển ( a^2 + 1 b )^7 số hạng thứ 5 là: - Tự Học 365] Trong khai triển \({\left( {{a^2} + {1 \over b}} \right)^7},\) số hạng thứ 5 là:
-
[ Cho biết tổng của các hệ số trong khai triển ( 1+2x )^n là 6561. Tìm n ? - Tự Học 365] Cho biết tổng của các hệ số trong khai triển \({{\left( 1+2x \right)}^{n}}\) là 6561. Tìm n ?
-
[Cho hình chóp S.ABCD có đáy ABCD là một tứ giác (AB và CD không song song). Gọi M là trung điểm của - Tự Học 365] Cho hình chóp S.ABCD có đáy ABCD là một tứ giác (AB và CD không song song). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB sao cho SN = 2NB, O là giao điểm của AC và BD. Giả sử đường thẳng d là giao tuyến của (SAC) và (SBD). Nhận xét nào sau đây là đúng?
-
[Cho hình chóp S.ABCD với đáy ABCD là tứ giác có các cặp cạnh đối không song song. Giả sử AC và BD cắ - Tự Học 365] Cho hình chóp S.ABCD với đáy ABCD là tứ giác có các cặp cạnh đối không song song. Giả sử AC và BD cắt nhau tại I. AD và BC cắt nhau tại O. Giao tuyến của hai mặt phẳng (SAC) và (SBD) là:
-
[Cho khai triển ( 1 - 2x )^n = a0 + a1x + a2x^2 + ... + anx^n. Tìm a5 biết a0 + a1 + a2 = 71. - Tự Học 365] Cho khai triển \({\left( {1 - 2x} \right)^n} = {a_0} + {a_1}x + {a_2}{x^2} + ... + {a_n}{x^n}\). Tìm \({a_5}\) biết \({a_0} + {a_1} + {a_2} = 71.\)
-
[ Cho hai đường thẳng a và b. Điều kiện nào sau đây đủ để kết luận a và b chéo nhau? - Tự Học 365] Cho hai đường thẳng a và b. Điều kiện nào sau đây đủ để kết luận a và b chéo nhau?
-
[Hệ số của số hạng chứa x^10 trong khai triển nhi thức ( x + 2 )^n biết n là số nguyên dương thỏa mãn - Tự Học 365] Hệ số của số hạng chứa \({x^{10}}\) trong khai triển nhi thức \({\left( {x + 2} \right)^n}\) biết n là số nguyên dương thỏa mãn \({3^n}C_n^0 - {3^{n - 1}}C_n^1 + {3^{n - 2}}C_n^2 - ... + {\left( { - 1} \right)^n}C_n^n = 2048\) là:
-
[Trong mp Oxy cho đường thẳng d : y = 3x. Ảnh của d qua phép quay tâm O góc quay a = 90o - Tự Học 365] Trong mp Oxy, cho đường thẳng d : y = 3x. Ảnh của d qua phép quay tâm O góc quay a = 90o
-
[Tìm hệ số của số hạng chứa x^8 trong khai triển nhị thức Newton của ( 1 x^3 + căn x^5 )^n biết C - Tự Học 365] Tìm hệ số của số hạng chứa \({x^8}\) trong khai triển nhị thức Newton của \({\left( {{1 \over {{x^3}}} + \sqrt {{x^5}} } \right)^n}\), biết \(C_{n + 4}^{n + 1} - C_{n + 3}^n = 7\left( {n + 3} \right)\)
-
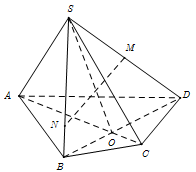
[ Cho hình chóp SABCD có đáy ABCD là một tứ giác (AB không song song với CD). Gọi M là trung điểm của - Tự Học 365] Cho hình chóp S,ABCD có đáy ABCD là một tứ giác (AB không song song với CD). Gọi M là trung điểm của SD, N là điểm nằm trên cạnh SB sao cho \(SN=2NB\), O là giao điểm của AC và BD. Cặp đường thẳng nào sau đây cắt nhau:
-
[ Cho tứ diện ABCD M thuộc đoạn AB thiết diện của hình chóp cắt bởi mặt phẳng ( alpha ) đi qua M son - Tự Học 365] Cho tứ diện ABCD, M thuộc đoạn AB, thiết diện của hình chóp cắt bởi mặt phẳng \(\left( \alpha \right)\) đi qua M song song với BD và AC là:
-
[Phương trình 1+2cos 2x=0 có nghiệm ( kin Z ) - Tự Học 365] Phương trình \(1+2\cos 2x=0\) có nghiệm \(\left( k\in Z \right)\)
