Toán11
Danh sách câu hỏi
-
[mathop lim limitsx to + giới hạn dx + 12x + 1 - Tự Học 365] \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{{x + 1}}{{2x + 1}}\)
-
[mathop lim limitsx to 3^ + d3x - 1x - 2. - Tự Học 365] \(\mathop {\lim }\limits_{x \to {3^ + }} \dfrac{{3x - 1}}{{x - 2}}\).
-
[ Tính giới hạn mathop lim limitsx to - giới hạn ( x^4 + 2x^2 + 1 ) : - Tự Học 365] Tính giới hạn \(\mathop {\lim }\limits_{x \to - \infty } \left( {{x^4} + 2{x^2} + 1} \right)\) :
-
[Cho tam giác đều A1B1C1 có độ dài cạnh bằng 4. Trung điểm của các cạnh tam giác A1B1C1 lập thành tam - Tự Học 365]
Cho tam giác đều \({A_1}{B_1}{C_1}\) có độ dài cạnh bằng 4. Trung điểm của các cạnh tam giác \({A_1}{B_1}{C_1}\) lập thành tam giác \({A_2}{B_2}{C_2}\), trung điểm các cạnh của \({A_2}{B_2}{C_2}\) lập thành tam giác \({A_3}{B_3}{C_3}\), …. Gọi \({P_1},\,\,{P_2},\,\,{P_3},...\) lần lượt là chu vi của tam giác \({A_1}{B_1}{C_1}, {A_2}{B_2}{C_2}, {A_3}{B_3}{C_3}\),… Tính tổng chu vi \(P = {P_1} + {P_2} + {P_3} + ...\)
-
[Cho hình chóp S.ABCD có đáy ABCD là hình thoi O là giao điểm của 2 đường chéo và SA = SC. Trong các - Tự Học 365] Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thoi, \(O\) là giao điểm của 2 đường chéo và \(SA = SC\). Trong các khẳng định sau, khẳng định nào đúng ?
-
[Cho hàm số y = f( x ) liên tục trên đoạn [ a;b ] và thỏa mãn f( a ) = bf( b ) = a với ab > 0a ne b. - Tự Học 365]
Cho hàm số \(y = f\left( x \right)\) liên tục trên đoạn \(\left[ {a;b} \right]\) và thỏa mãn \(f\left( a \right) = b,\,\,f\left( b \right) = a\) với \(a,b > 0,\,\,a \ne b\). Khi đó phương trình nào sau đây có nghiệm trên khoảng \(\left( {a;b} \right)\).
-
[Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật với AB = aAD = 2aSA = a và SA bot ( ABCD ). Gọi MN - Tự Học 365]
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật với \(AB = a,\,\,AD = 2a,\,\,SA = a\) và \(SA \bot \left( {ABCD} \right)\). Gọi \(M,N\) lần lượt là trung điểm của \(AB\) và \(CD\). Tính khoảng cách giữa đường thẳng \(MD\) và mặt phẳng \(\left( {SBN} \right)\).
-
[Một bình nuôi cấy vi sinh vật được giữ ở nhiệt độ 0^0C. Tại thời điểm t = 0 người ta cung cấp nhiệt - Tự Học 365]
Một bình nuôi cấy vi sinh vật được giữ ở nhiệt độ \({0^0}C\). Tại thời điểm \(t = 0\) người ta cung cấp nhiệt cho nó. Nhiệt độ của bình bắt đầu tăng lên và tại mỗi thời điểm \(t\), nhiệt độ của nó được ước tính bởi hàm số \(f\left( t \right) = {\left( {t - 1} \right)^3} + 1\,\,\left( {^0C} \right)\). Hãy so sánh tốc độ tăng nhiệt độ của bình tại hai thời điểm \({t_1} = 0,5s\) và \({t_2} = 1,25s\).
-
[Trong các khẳng định dưới đây có bao nhiêu khẳng định đúng ?
Trong các khẳng định dưới đây, có bao nhiêu khẳng định đúng ?
(1) \(\lim {n^k} = + \infty \) với \(k\) nguyên dương
(2) \(\lim {q^n} = + \infty \) nếu \(\left| q \right| < 1\).
(3) \(\lim {q^n} = + \infty \) nếu \(q > 1\)
-
[Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh aSA vuông góc với mặt phẳng ( ABCD ) và SA = a . - Tự Học 365]
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông cạnh \(a,\,\,SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\) và \(SA = a\) . Góc giữa 2 mặt phẳng \(\left( {SAD} \right)\) và \(\left( {SBC} \right)\) bằng :
-
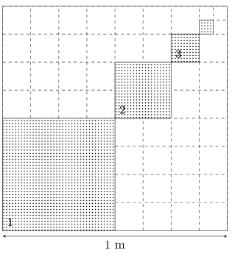
[Để trang trí cho quán trà sữa sắp mở của mình bạn Việt quyết định tô màu một mảng tường hình vuông c - Tự Học 365] Để trang trí cho quán trà sữa sắp mở của mình, bạn Việt quyết định tô màu một mảng tường hình vuông cạnh bằng \(1m\). Phần tô màu dự kiến là các hình vuông nhỏ được đánh số lần lượt là \(1,2,3,...,n,...\) (các hình vuông được tô chấm bi), trong đó cạnh của hình vuông kế tiếp bằng một nửa cạnh hình vuông trước đó (hình vẽ). Giả sử quy trình tô màu của Việt có thể diễn ra nhiều giờ. Hỏi bạn Việt tô màu đến hình vuông thứ mấy thì diện tích của hình vuông được tô bắt đầu nhỏ hơn \(\dfrac{1}{{1000}}{m^2}\)?