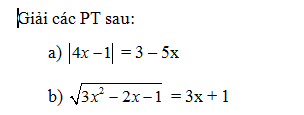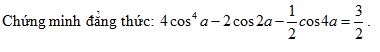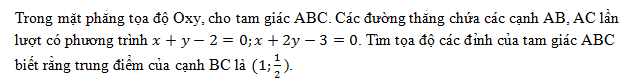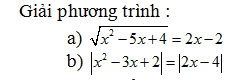Toán 10
Danh sách câu hỏi
-
[Cho hình vuông ABCD.AB,BC,CD,DA lần lượt đi qua M( 3;0 );N( 6;6 );P( 5 - Tự Học 365] Cho hình vuông \(ABCD.\,\,AB,\,\,BC,\,\,CD,\,\,DA\) lần lượt đi qua \(M\left( {3;0} \right);\,\,N\left( {6;6} \right);\,\,P\left( {5;9} \right);\,\,Q\left( { - 5;4} \right)\). Lập phương trình AB, BC.
-
[BAN CƠ BẢN - Tự Học 365] BAN CƠ BẢN

-
[(Học sinh tự chứng minh). Tứ giác ABCD có I, J là trung điểm của AC, B - Tự Học 365] (Học sinh tự chứng minh). Tứ giác ABCD có I, J là trung điểm của AC, BD. Chứng minh \(\overrightarrow {AB} + \overrightarrow {CD} = 2\overrightarrow {IJ} \)
-
[Cho tam giác ABC có phương trình ( AB ):x + y + 5 = 0. Phương trình ( - Tự Học 365] Cho tam giác ABC có phương trình \(\left( {AB} \right):\,\,x + y + 5 = 0\). Phương trình \(\left( {AC} \right):\,\,3x + 2y - 1 = 0\). Trọng tâm \(G\left( {1;3} \right).\) Lập phương trình BC.
-
[a) Cho tứ giác ABCD. Chứng minh rằng: rightarrow AB + rightarrow CD - Tự Học 365] a) Cho tứ giác ABCD. Chứng minh rằng: \(\overrightarrow {AB} + \overrightarrow {CD} = \overrightarrow {AD} - \overrightarrow {BC} \).
b) Cho DABC có trọng tâm G. Gọi M, N là các điểm xác định bởi \(\overrightarrow {AM} = 2\overrightarrow {AB} \), \(\overrightarrow {AN} = \dfrac{2}{5}\overrightarrow {AC} \). Chứng minh rằng: M, N, G thẳng hàng.