Toán 10
Danh sách câu hỏi
-
[Cho 4 số không âm a,b,c,d. Chứng minh rằng: - Tự Học 365] Cho 4 số không âm a,b,c,d. Chứng minh rằng:
-
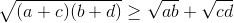
[Cho các điểm A, B, C, D, E. a. Tìm O sao cho - Tự Học 365] Cho các điểm A, B, C, D, E.
a. Tìm O sao cho
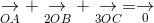
ightarrow} + underset{2OB}{
ightarrow} + underset{3OC}{
ightarrow} = underset{0}{
ightarrow}" align="absmiddle" />
b. Tìm I sao cho
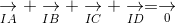
ightarrow} + underset{IB}{
ightarrow} + underset{IC}{
ightarrow} + underset{ID}{
ightarrow}= underset{0}{
ightarrow}" align="absmiddle" />
c. Tìm K sao cho
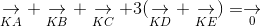
ightarrow} + underset{KB}{
ightarrow} + underset{KC}{
ightarrow} + 3(underset{KD}{
ightarrow} + underset{KE}{
ightarrow}) = underset{0}{
ightarrow}" align="absmiddle" /> -
[Cho - Tự Học 365] Cho
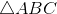. Gọi M là trung điểm của AB và N là một điểm trên cạnh AC, sao cho NC = 2NA.
a. Xác định điểm K sao cho
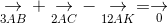
ightarrow} + underset{2AC}{
ightarrow} - underset{12AK}{
ightarrow} = underset{0}{
ightarrow}" align="absmiddle" /> (1)
b. Xác định điểm D sao cho
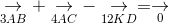
ightarrow} + underset{4AC}{
ightarrow} - underset{12KD}{
ightarrow} = underset{0}{
ightarrow}" align="absmiddle" /> (2) -
[Cho tứ giác ABCD, M là điểm tùy ý. Trong mỗi trường hợp hãy tìm số k v - Tự Học 365] Cho tứ giác ABCD, M là điểm tùy ý. Trong mỗi trường hợp hãy tìm số k và điểm cố định I, J, K sao cho các đẳng thức vectơ sau thỏa mãn với mọi điểm M.
a.
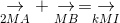
ightarrow} + underset{MB}{
ightarrow} = underset{kMI}{
ightarrow}" align="absmiddle" /> (1)
b.
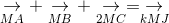
ightarrow} + underset{MB}{
ightarrow} + underset{2MC}{
ightarrow} = underset{kMJ}{
ightarrow}" align="absmiddle" /> (2)
c.
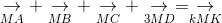
ightarrow} + underset{MB}{
ightarrow} + underset{MC}{
ightarrow} + underset{3MD}{
ightarrow}= underset{kMK}{
ightarrow}" align="absmiddle" /> (3) -
[Cho hình bình hành ABCD tâm O. Lấy các điểm I, J sao cho: - Tự Học 365] Cho hình bình hành ABCD tâm O. Lấy các điểm I, J sao cho:
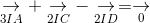
ightarrow} + underset{2IC}{
ightarrow} - underset{2ID}{
ightarrow} = underset{0}{
ightarrow}" align="absmiddle" /> (1)
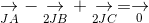
ightarrow} - underset{2JB}{
ightarrow} + underset{2JC}{
ightarrow} = underset{0}{
ightarrow}" align="absmiddle" /> (2)
Chứng minh rằng I, J, O thẳng hàng.
-
[Cho - Tự Học 365] Cho
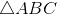, lấy các điểm I, J thỏa mãn:
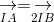
ightarrow} = underset{2IB}{
ightarrow}" align="absmiddle" /> (1)
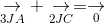
ightarrow} + underset{2JC}{
ightarrow} = underset{0}{
ightarrow}" align="absmiddle" /> (2)
Chứng minh rằng IJ đi qua trọng tâm G của
. -
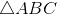[Cho - Tự Học 365] Cho
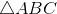, điểm M trong mặt phẳng thỏa mãn:
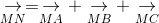
ightarrow} = underset{MA}{
ightarrow} + underset{MB}{
ightarrow} + underset{MC}{
ightarrow}" align="absmiddle" />
a. Chứng minh rằng MN luôn đi qua trọng tâm G của
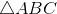khi M thay đổi.
b. Gọi P là trung điểm của CN. Chứng minh rằng MP luôn đi qua một điểm cố định khi M thay đổi.
-
[Chứng minh rằng : - Tự Học 365] Chứng minh rằng :
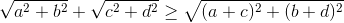(1) -
[Cho 4 điểm A, B, C, D. Chứng minh rằng: - Tự Học 365] Cho 4 điểm A, B, C, D. Chứng minh rằng:
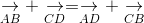
ightarrow} + underset{CD}{
ightarrow} = underset{AD}{
ightarrow} + underset{CB}{
ightarrow}" align="absmiddle" /> -
[Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng: - Tự Học 365] Cho 6 điểm A, B, C, D, E, F. Chứng minh rằng:
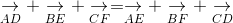
ightarrow} + underset{BE}{
ightarrow} + underset{CF}{
ightarrow} = underset{AE}{
ightarrow} + underset{BF}{
ightarrow} + underset{CD}{
ightarrow}" align="absmiddle" />
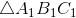và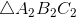 
lần lượt có trọng tâm là 
, 
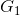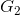. Chứng minh rằng: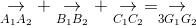 
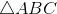. Gọi M là một điểm trên đoạn BC, sao cho: MB = 2MC. Chứng minh rằng: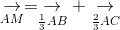 
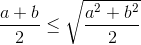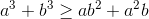
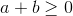
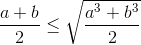(1)
(1)