Toán 10
Danh sách câu hỏi
-
[Cho phương trình : - Tự Học 365] Cho phương trình :
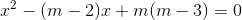(1)
1) Tìm m để (1) có 2 nghiệm thỏa mãn
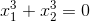
2) Chứng minh rằng nếu (1) có 1 nghiệm duwong là x1 thì phương trình :
(*) cũng có 1 nghiệm dương là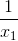 
-
[Cho - Tự Học 365] Cho
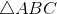đều cạnh a, trọng tâm G.
a. Tính các tích vô hướng:
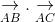
ightarrow}.underset{AC}{
ightarrow}" align="absmiddle" /> và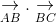
ightarrow}.underset{BC}{
ightarrow}" align="absmiddle" />.
b. Gọi I là điểm thỏa mãn
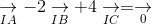
ightarrow} - 2underset{IB}{
ightarrow} + 4underset{IC}{
ightarrow} = underset{0}{
ightarrow}" align="absmiddle" />. Chứng minh rằng BCIG là hình bình hành, từ đó tính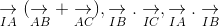
ightarrow}(underset{AB}{
ightarrow} + underset{AC}{
ightarrow}), underset{IB}{
ightarrow}.underset{IC}{
ightarrow}, underset{IA}{
ightarrow}.underset{IB}{
ightarrow}" align="absmiddle" />. -
[So sánh số a = -1 với các nghiệm của phương trình : f(x) = (m – 1)x2 - Tự Học 365] So sánh số a = -1 với các nghiệm của phương trình :
f(x) = (m – 1)x2 –mx – 2(m+1) = 0 (1)
-
[Cho 4 điểm A, B, C, D. Chứng minh rằng AB vuông góc với CD khi và chỉ - Tự Học 365] Cho 4 điểm A, B, C, D. Chứng minh rằng AB vuông góc với CD khi và chỉ khi:
(1) -
[So sánh số a = 1 với các nghiệm của phương trình : f(x) = (3 – m)x2 – - Tự Học 365] So sánh số a = 1 với các nghiệm của phương trình :
f(x) = (3 – m)x2 –2(2m – 1)x – 2m+5 (1)
-
[Cho hình bình hành ABCD, biết rằng với mọi điểm M luôn có: - Tự Học 365] Cho hình bình hành ABCD, biết rằng với mọi điểm M luôn có:
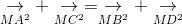
ightarrow} + underset{MC^{2}}{
ightarrow} = underset{MB^{2}}{
ightarrow} + underset{MD^{2}}{
ightarrow}" align="absmiddle" /> (1)
Chứng minh rằng ABCD là hình chữ nhật.
-
[Cho hình bình hành ABCD, tâm O, M là điểm tùy ý. a. Chứng minh rằng: - Tự Học 365] Cho hình bình hành ABCD, tâm O, M là điểm tùy ý.
a. Chứng minh rằng:
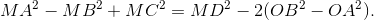
b. Giả sử M di động trên đường tròn (d), xác định vị trí của M để:
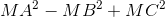đạt giá trị nhỏ nhất. -
[Cho 6x + y = 5 . Chứng minh rằng : - Tự Học 365] Cho 6x + y = 5 . Chứng minh rằng :
-
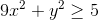
[Cho - Tự Học 365] Cho
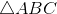, biết A(1, 2), B (-1, 1), C(5, -1).
a. Tính
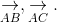
ightarrow}, underset{AC}{
ightarrow}." align="absmiddle" />
b. Tính cos và sin góc A.
c. Tìm tọa độ chân đường cao
của .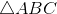
d Tìm tọa độ trực tâm H của
.
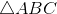e. Tìm tọa độ trọng tâm G của
.
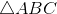f. Tìm tọa độ tâm I của đường tròn ngoại tiếp
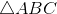, từ đó chứng minh rằng I, H, G thẳng hàng. -
[Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm AB, AC, BC. - Tự Học 365] Cho tam giác ABC. Các điểm M, N, P lần lượt là trung điểm AB, AC, BC. Chứng mình rằng với điểm O bất kì ta có:
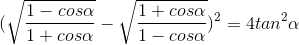
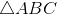vuông tại A, gọi M là trung điểm BC. Lấy các điểm 
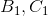trên AB và AC sao cho 
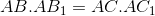. Chứng minh rằng: AM vuông góc với 
.
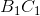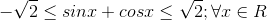
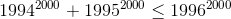(1)