Toán 10
Danh sách câu hỏi
-
[Cho a730 - Tự Học 365] Cho
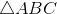có AB = 5, AC = 6, BC = 7. Gọi trung điểm của AC là M. Tính bán kính đường tròn ngoại tiếp 
. -
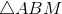[Cho a731 - Tự Học 365] Cho
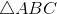có AB = 3, AC = 4 và diện tích S = 
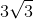. Tính BC. -
[Cho a732 - Tự Học 365] Cho
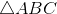vuông tại A, 
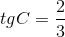và đường cao AH = 6. Tính độ dài các đọn HB, HC, AB, AC. -
[Cho a734 - Tự Học 365] Cho
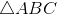có AB = 2, AC = 3, BC = 4. Tính:a. Diện tích S của tam giác.
b. Các đường cao
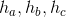.c. Các bán kính R, r.
-
[Cho a680 - Tự Học 365] Cho
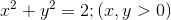. Tìm giá trị nhỏ nhất của :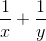 
-
[Cho a735 - Tự Học 365] Cho
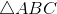cân tại A. Đường cao BH = a, 
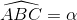.a. Tính các cạnh và đường cao còn lại.
b. Tính bán kính đường tròn nội tiếp và ngoại tiếp
. -
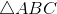[Cho a682 - Tự Học 365] Cho
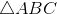, biết A(1, -3). B(3, -5), C(2, -2). Tìm tọa độ:a. Giao điểm E của BC với phân giác trong của góc A.
b. Giao điểm F của BC với phân giác ngoài của góc A.
-
[Cho a736 - Tự Học 365] Cho
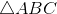, các trung tuyến 
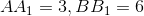và hợp với nhau một góc 
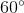. Tính độ dài các cạnh của . -
[Cho a707 - Tự Học 365] Cho
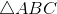vuông tại A, biết 
. Tính các góc:
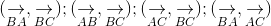ightarrow}, underset{BC}{
ightarrow}); (underset{AB}{
ightarrow}, underset{BC}{
ightarrow}); (underset{AC}{
ightarrow}, underset{BC}{
ightarrow});(underset{BA}{
ightarrow}, underset{AC}{
ightarrow})" align="absmiddle" />. -
[Cho a737 - Tự Học 365] Cho
, biết AB = 2, BC = 3, CA = 4., đường cao AD. Tính độ dài đoạn CD. -
[Cho a722 - Tự Học 365] Cho
vuông tại A, biết 
. Tính các góc:
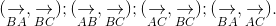ightarrow}, underset{BC}{
ightarrow}); (underset{AB}{
ightarrow}, underset{BC}{
ightarrow}); (underset{AC}{
ightarrow}, underset{BC}{
ightarrow}); (underset{BA}{
ightarrow}, underset{AC}{
ightarrow})." align="absmiddle" /> -
[Cho a738 - Tự Học 365] Cho
có diện tích 12. Trên các cạnh AB, AC lần lượt lấy các điểm M, N sao cho: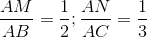 
và BN cắt CM tại N.a. Tính diện tích tam giác BMC, ABN và AMN theo
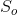.b. Tính tỉ số diện tích của hai tam giác ACD và BCD; ABD và BCD.
c. Suy ra diện tích của tam giác BCD theo
. -
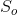[Cho a728 - Tự Học 365] Cho
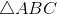, biết 
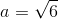, b=2, 
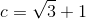. Tính các góc A, B, C và đường cao 
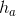của tam giác. -
[Cho a729 - Tự Học 365] Cho
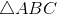, biết b=7, c=5, 
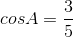. Tính đường cao 
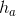và bán kính đường tròn ngoại tiếp R của tam giác.
vuông, có cạnh huyền 
, M là trung điểm BC. Biết rằng: 
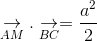ightarrow}.underset{BC}{
ightarrow} = frac{a^{2}}{2}" align="absmiddle" />, tính độ dài AB và AC.