Xác định m để : x2 – 2x + 1 – m2 ≤ 0 t

Câu hỏi
Nhận biếtXác định m để : x2 – 2x + 1 – m2 ≤ 0 thỏa mãn với x ε [1 , 2]
Đáp án đúng: D
Lời giải của Tự Học 365
Lời giải chi tiết:
Đặt f(x) = x2 – 2x + 1 – m2
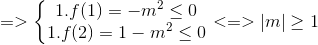
Chọn D

Xác định m để : x2 – 2x + 1 – m2 ≤ 0 thỏa mãn với x ε [1 , 2]
Lời giải chi tiết:
Đặt f(x) = x2 – 2x + 1 – m2
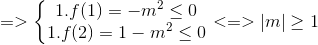
Chọn D





