vẽ hai tiếp tuyến AB, AC của đường tròn (B, C là hai tiếp điểm). Gọi

Câu hỏi
Nhận biếtQua điểm A nằm ngoài đường tròn \(\left( O \right)\) vẽ hai tiếp tuyến AB, AC của đường tròn (B, C là hai tiếp điểm). Gọi E là trung điểm của AC, F là giao điểm thứ hai của EB với đường tròn \(\left( O \right)\).
a) Chứng minh: tứ giác \(ABOC\) là tứ giác nội tiếp, tam giác \(CEF\) đồng dạng với tam giác \(BEC\).
b) Gọi K là giao điểm thứ hai của đường thẳng AF với đường tròn \(\left( O \right)\). Chứng minh \(BF.CK = BK.CF\).
c) Chứng minh AE là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
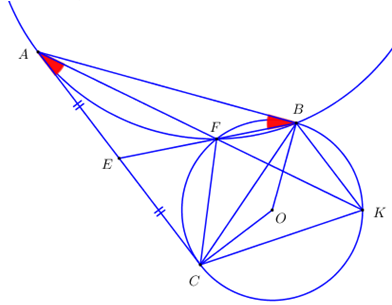
a) Chứng minh: tứ giác \(ABOC\) là tứ giác nội tiếp, tam giác \(CEF\) đồng dạng với tam giác \(BEC\).
+) Chứng minh: tứ giác \(ABOC\) là tứ giác nội tiếp:
Do \(AB,\,\,AC\) là tiếp tuyến của \(\left( O \right)\,\,\left( {gt} \right) \Rightarrow AB \bot OB;\,\,AC \bot OC \Rightarrow \angle OBA = \angle OCA = {90^0}\).
Xét tứ giác \(ABOC\) có: \(\angle OBA + \angle OCA = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(ABOC\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
+) Chứng minh \(\Delta CEF \sim \Delta BEC\)
Xét đường tròn \(\left( O \right)\) ta có:
\(\angle EOF\) là góc tạo bởi tia tiếp tuyến và dây cung chắn cung \(CF.\)
\(\angle FBC\) là góc nội tiếp chắn cung \(CF.\)
\( \Rightarrow \angle ECF = \angle CBF\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung \(CF\))
Xét \(\Delta CEF\) và \(\Delta BEC\) ta có:
\(\begin{array}{l}\angle E\,\,chung\\\angle ECF = \angle EBC\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta CEF \sim \Delta BEC\,\,\left( {g - g} \right).\,\,\,\left( {dpcm} \right)\end{array}\)
b) Gọi K là giao điểm thứ hai của đường thẳng AF với đường tròn \(\left( O \right)\). Chứng minh \(BF.CK = BK.CF\).
Xét tam giác \(ABF\) và tam giác \(AKB\) có:
\(\angle BAK\,\,\,chung\)
\(\angle ABF = \angle AKB\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(BF\));
\( \Rightarrow \Delta ABF \sim \Delta AKB\,\,\left( {g.g} \right) \Rightarrow \frac{{BF}}{{BK}} = \frac{{AF}}{{AB}}\,\,\left( 1 \right)\) (các cặp cạnh tương ứng tỉ lệ).
Xét tam giác \(ACF\) và tam giác \(AKC\) có:
\(\angle CAK\) chung;
\(\angle ACF = \angle AKC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(CF\));
\( \Rightarrow \Delta ACF \sim \Delta AKC\,\,\left( {g.g} \right) \Rightarrow \frac{{CF}}{{CK}} = \frac{{AF}}{{AC}}\,\,\left( 2 \right)\) (các cặp cạnh tương ứng tỉ lệ).
Mà \(AB = AC\) (tính chất 2 tiếp tuyến cắt nhau) nên \(\frac{{AF}}{{AB}} = \frac{{AF}}{{AC}}\) (3).
Từ (1), (2) và (3) suy ra \(\frac{{BF}}{{BK}} = \frac{{CF}}{{CK}} \Rightarrow BF.CK = BK.CF\).
c) Chứng minh AE là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).
Xét tam giác \(ECF\) và ta giác \(EBC\) có:
\(\angle BEC\) chung;
\(\angle ECF = \angle EBC\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung \(CF\))
\( \Rightarrow \Delta ECF \sim \Delta EBC\,\,\left( {g.g} \right) \Rightarrow \frac{{EC}}{{EB}} = \frac{{EF}}{{EC}} \Rightarrow E{C^2} = EB.EF\).
Mà \(EC = EA\,\,\left( {gt} \right) \Rightarrow E{A^2} = EB.EF \Rightarrow \frac{{EA}}{{EB}} = \frac{{EF}}{{EA}}\).
Xét tam giác \(BEA\) và tam giác \(AEF\) có:
\(\begin{array}{l}\frac{{EA}}{{EB}} = \frac{{EF}}{{EA}}\,\,\left( {cmt} \right)\\\angle AEB\,\,\,\,chung\end{array}\)
\( \Rightarrow \Delta BEA \sim \Delta AEF\,\,\left( {c - g - c} \right) \Rightarrow \angle ABE = \angle FAE\) (hai góc tương ứng)
Mà góc \(\angle ABE\) là góc nội tiếp chắn cung \(AF\) của đường tròn ngoại tiếp tam giác \(ABF\); \(\angle FAE\) ở vị trí góc tạo bởi tiếp tuyến và dây cung chắn cung \(AF\)).
Vậy \(AE\) là tiếp tuyến của đường tròn ngoại tiếp tam giác \(ABF\).

