Vẽ CH vuông góc với AB (H ϵ AB). Chứng minh rằng MB đi qua trung điểm của CH.
Câu hỏi
Nhận biếtVẽ CH vuông góc với AB (H ϵ AB). Chứng minh rằng MB đi qua trung điểm của CH.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Tia BC cắt Ax tại N. Ta có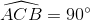 
(góc nội tiếp chắn nửa đường tròn)
=> 
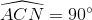, suy ra ∆ACN vuông tại C. Lại có MC = MA nên suy ra được MC = MN, do đó MA = MN (5).
Mặt khác ta có CH // NA (cùng vuông góc với AB) nên theo định lí Ta-lét thì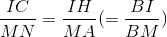 
(6).
Từ (5) và (6) suy ra IC = IH hay MB đi qua trung điểm của CH.
