Tứ giác ABCD nội tiếp đường tròn có hai cạnh đối AB và CD cắt nhau tại M và góc BAD=80^0 thì góc BCM

Câu hỏi
Nhận biếtTứ giác ABCD nội tiếp đường tròn có hai cạnh đối AB và CD cắt nhau tại M và \(\widehat{BAD}={{80}^{0}}\) thì \(\widehat{BCM}=?\)
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
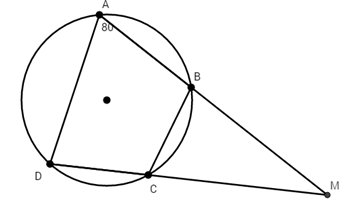
Tứ giác ABCD nội tiếp nên có:
\(\begin{align} & \widehat{DAB}+\widehat{BCD}={{180}^{0}} \\ & \Rightarrow \widehat{BCD}={{180}^{0}}-{{80}^{0}}={{100}^{0}} \\ \end{align}\)
Mà \(\widehat{BCD}+\widehat{BCM}={{180}^{0}}\)(kề bù)
\(\Rightarrow \widehat{BCM}={{180}^{0}}-{{100}^{0}}={{80}^{0}}\)
Chọn C

