Tứ giác ABCD có chu vi 18cmAB = 34BCCD = 54BC và AD = 2AB. Tính độ dài các cạnh của tứ giác ABCD. Bi

Câu hỏi
Nhận biếtTứ giác \(ABCD\) có chu vi \(18cm,\,\,\,AB = \frac{3}{4}BC,\,\,CD = \frac{5}{4}BC\) và \(AD = 2AB.\) Tính độ dài các cạnh của tứ giác \(ABCD.\) Biết \(AC = CD,\) tính diện tích tứ giác \(ABCD.\)
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
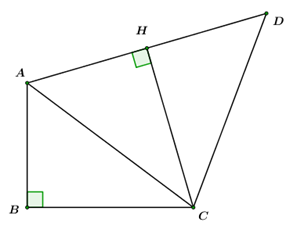
Theo đề bài ta có: \(\left\{ \begin{array}{l}AB = \frac{3}{4}BC\\CD = \frac{5}{4}BC\\AD = 2AB\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AB = \frac{3}{4}BC\\CD = \frac{5}{4}BC\\AD = 2.\frac{3}{4}BC = \frac{3}{2}BC\end{array} \right..\)
Lại có chu vi tứ giác \(ABCD\) là \(18cm\) nên ta có:
\(\begin{array}{l}AB + BC + CD + DA = 18\\ \Leftrightarrow \frac{3}{4}BC + BC + \frac{5}{4}BC + \frac{3}{2}BC = 18\\ \Leftrightarrow \frac{9}{2}BC = 18 \Leftrightarrow BC = 4\,\,cm.\\ \Rightarrow \left\{ \begin{array}{l}AB = \frac{3}{4}.4 = 3\,\,cm\\CD = \frac{5}{4}.4 = 5\,\,cm\\AD = \frac{3}{2}.4 = 6\,\,cm.\end{array} \right.\end{array}\)
Theo đề bài ta có: \(AC = CD = 5cm\)
Ta có: \(\left\{ \begin{array}{l}A{B^2} + B{C^2} = {3^2} + {4^2} = 25\\A{C^2} = {5^2} = 25\end{array} \right. \Rightarrow \Delta ABC\) vuông tại \(B\) (theo định lý Pi-ta-go đảo).
\( \Rightarrow {S_{ABC}} = \frac{1}{2}AB.BC = \frac{1}{2}.3.4 = 6\,\,c{m^2}.\)
Xét \(\Delta ACD\) ta có: \(AC = CD = 5cm \Rightarrow \Delta ACD\) là tam giác cân tại \(C.\)
Kẻ đường cao \(CH\,\,\left( {H \in AD} \right)\) của \(\Delta ACD \Rightarrow H\) là trung điểm của \(AD \Rightarrow AH = HD = \frac{1}{2}.6 = 3cm.\)
Áp dụng định lý Pi-ta-go với \(\Delta AHC\) vuông tại \(H\) ta có:
\(\begin{array}{l}CH = \sqrt {A{C^2} - H{A^2}} = \sqrt {{5^2} - {3^2}} = 4.\\ \Rightarrow {S_{ACD}} = \frac{1}{2}CH.AD = \frac{1}{2}.4.6 = 12\,\,c{m^2}.\\ \Rightarrow {S_{ABCD}} = {S_{ABC}} + {S_{ACD}} = 6 + 12 = 18c{m^2}.\end{array}\)
Chọn D.

