, từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB (A, B

Câu hỏi
Nhận biếtCho đường tròn tâm (O), từ điểm M ở bên ngoài đường tròn (O) kẻ các tiếp tuyến MA, MB (A, B là các tiếp điểm), kẻ cát tuyến MCD không đi qua tâm O (C nằm giữa M và D; O và B nằm về hai phía so với cát tuyến MCD).
a) Chứng minh tứ giác MAOB nội tiếp.
b) Chứng minh \(M{{B}^{2}}=MC.MD\)
c) Gọi H là giao điểm của AB và OM. Chứng minh AB là phân giác của \(\widehat{CHD}\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
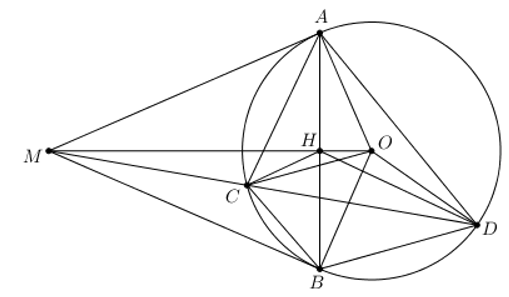
a) Chứng minh tứ giác MAOB nội tiếp.
Ta có \(\widehat{OAM}=\widehat{OBM}={{90}^{0}}\) (Do MA, MB là tiếp tuyến của đường tròn (O))
Xét tứ giác OAMB có: \(\widehat{OAM}+\widehat{OBM}={{90}^{0}}+{{90}^{0}}={{180}^{0}}\Rightarrow\) Tứ giác OAMB là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Chứng minh \(M{{B}^{2}}=MC.MD\)
Xét tam giác MBC và tam giác MDB có:
\(\widehat{BMD}\) chung;
\(\widehat{MBC}=\widehat{MDB}\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung BC)
\(\Rightarrow \Delta MBC\backsim \Delta MDB\,\,\left( g.g \right)\Rightarrow \frac{MB}{MD}=\frac{MC}{MB}\Rightarrow M{{B}^{2}}=MC.MD\)
c) Gọi H là giao điểm của AB và OM. Chứng minh AB là phân giác của \(\widehat{CHD}\).
Ta có \(MA=MB\) (tính chất hai tiếp tuyến cắt nhau) \(\Rightarrow M\) thuộc trung trực của AB;
\(OA=OB\,\,\left( =R \right)\Rightarrow O\) thuộc trung trực của AB;
\(\Rightarrow OM\) là trung trực của AB \(\Rightarrow OM\bot AB\)
Xét tam giác vuông OMB có \(M{{B}^{2}}=MH.MO\) (hệ thức lượng trong tam giác vuông).
Mà \(M{{B}^{2}}=MC.MD\,\,\left( cmt \right)\Rightarrow MH.MO=MC.MD\Rightarrow \frac{MC}{MO}=\frac{MH}{MD}\)
Xét tam giác MCH và MOD có :
\(\widehat{OMD}\) chung ;
\(\frac{MC}{MO}=\frac{MH}{MD}\,\,\,\left( cmt \right)\);
\(\Delta MCH\backsim \Delta MOD\,\,\left( c.g.c \right)\Rightarrow \widehat{MHC}=\widehat{MDO}\) (hai góc tương ứng) (1).
Mà \(\widehat{MHC}+\widehat{OHC}={{180}^{0}}\Rightarrow \widehat{MDO}+\widehat{OHC}={{180}^{0}}\Rightarrow\) Tứ giác OHCD là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
\(\Rightarrow \widehat{OHD}=\widehat{OCD}\) (2) (hai góc nội tiếp cùng chắn cung OD).
Mà \(\widehat{OCD}=\widehat{ODC}=\widehat{MDO}\) (3) (tam giác OCD cân tại O);
Từ (1), (2) và (3) \(\Rightarrow \widehat{MHC}=\widehat{OHD}\).
\(\Rightarrow {{90}^{0}}-\widehat{MHC}={{90}^{0}}-\widehat{OHD}\Rightarrow \widehat{CHB}=\widehat{BHD}\).
Vậy HB là tia phân giác của góc CHD hay AB là tia phân giác của góc CHD.

